Tipo de funciones - Funciones racionales

1.- Funciones racionales

Son aquellas que son del tipo: y = P(x) / Q (x), siendo P(x) y Q(x) dos polinomios (y Q(x) de grado ≥ 1)

Y = (3x² – 7) / (4x² + 8)

El dominio de estas funciones son todos los números reales R (- ∞; ∞) a excepción de aquellos que hagan 0 el denominador,

Dentro de las funciones racionales distinguimos:

a) Funciones racionales del tipo y = k / x (siendo k una constante)

Se denominan funciones de proporcionalidad inversa.

y = 7 / x

y = 3 / x

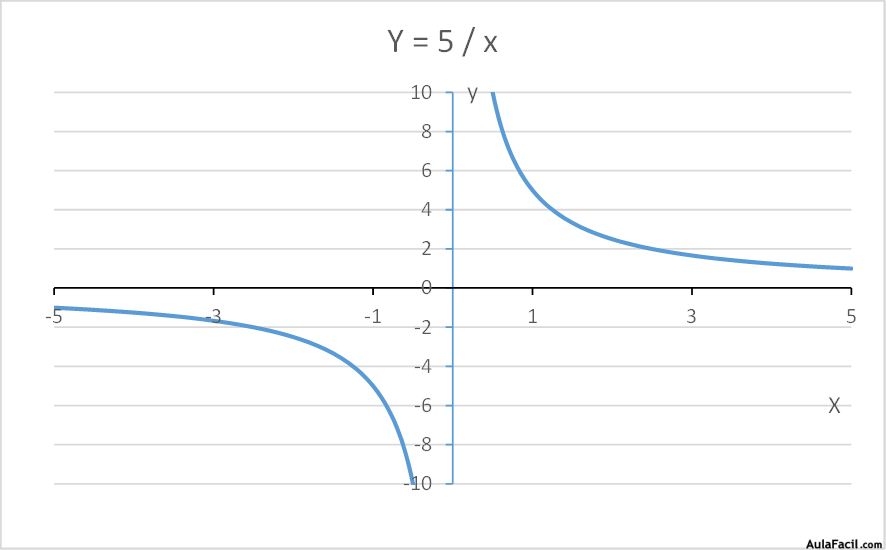
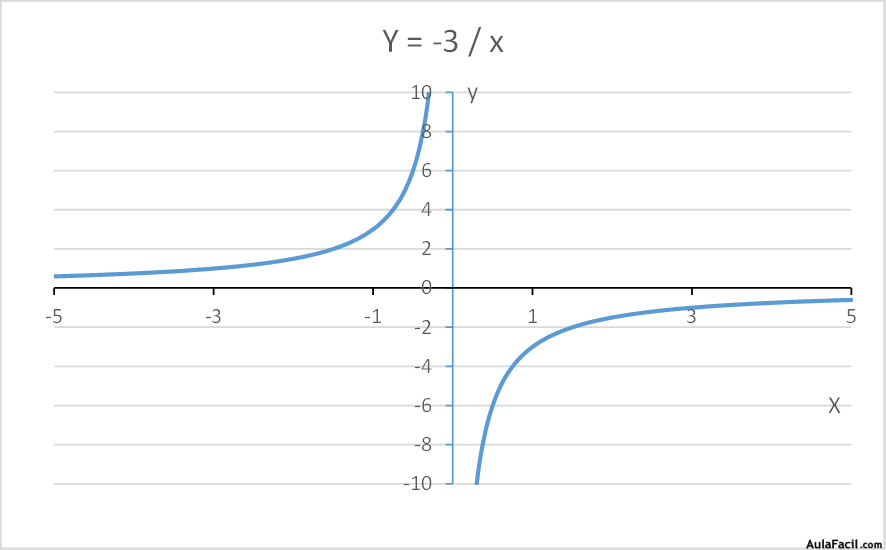
Su representación gráfica tiene forma de hipérbola:

Si la constante es positiva se sitúa en el cuadrante derecho superior e izquierdo inferior, mientras que si la constante es negativa se sitúa en los otros dos cuadrantes.

Características de estas funciones:

1.- Dominio: el conjunto de números reales R [(- ∞; ∞) – 0]; es decir, todos los números reales a excepción de 0 ya que anula el denominador dando error en la función.

2.- Función continua en todo su dominio a excepción de un punto de corte en x = 0.

3.- Recorrido: R [(- ∞; ∞) – 0]. Cuando x tiende a - ∞ / ∞, la variable dependiente “y” se acerca a 0 pero sin llegar a tocarlo.

4.- La función es asintótica respecto a los ejes de abscisas y ordenadas: cuando x tiende a - ∞ / ∞ la variable dependiente “y” tiende a 0, mientras que cuando x tiende a 0 la variable dependiente “y” tiende a - ∞ / ∞.

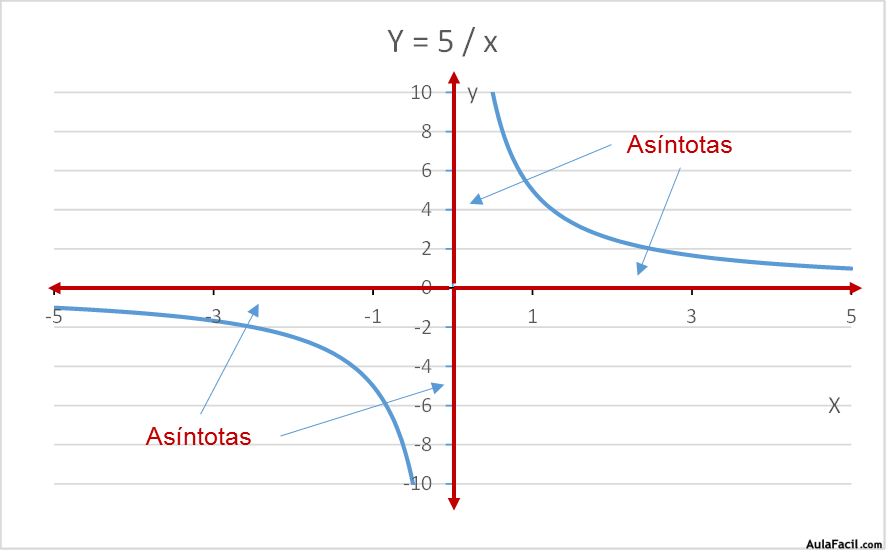
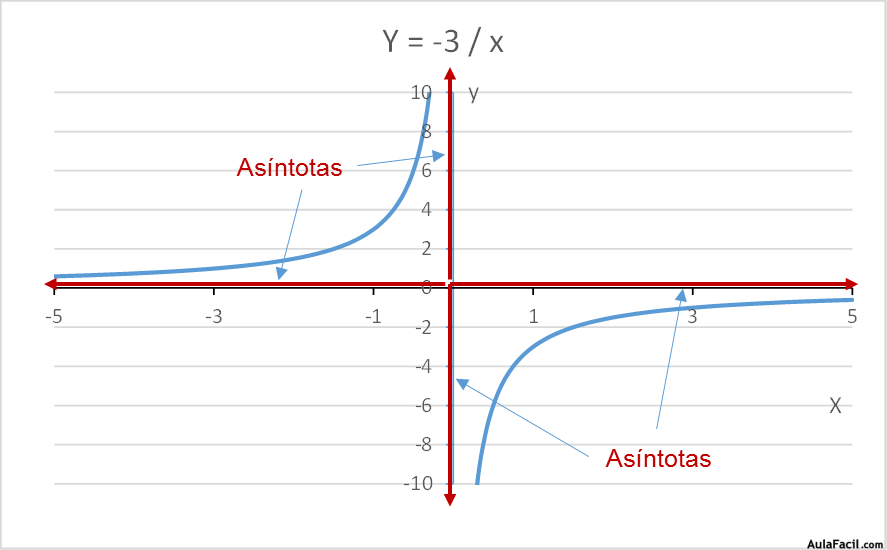
5.- Función impar (simétrica respecto al origen de coordenadas).

Veamos algunos tipos de función derivadas de este modelo:

1.- Funciones racionales del tipo y = (k / x) + a (siendo a un número real)

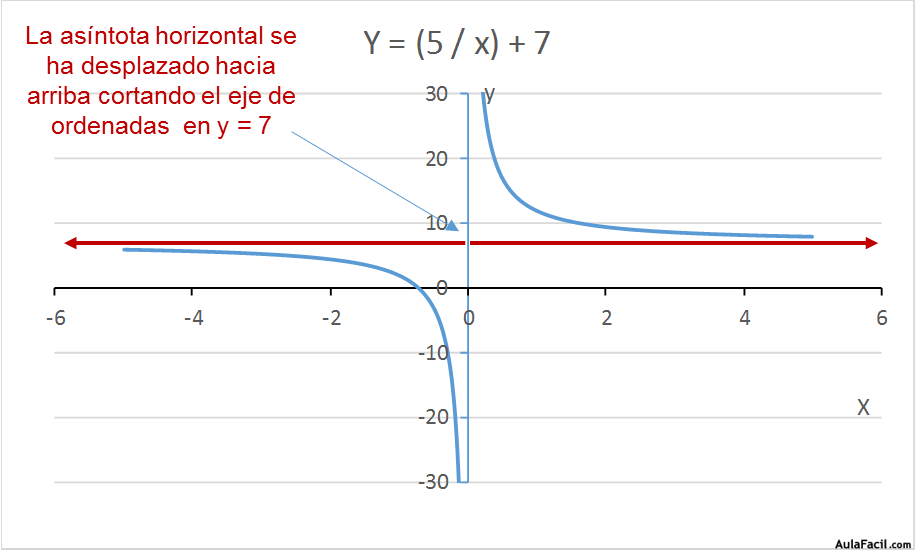
La gráfica de esta función es similar a la de la función de proporcionalidad inversa, simplemente se habrá desplazado hacia arriba o hacia abajo dependiendo de que el número “a” sea positivo o negativo.

y = (7 / x) + 5

y = (7 / x) -10

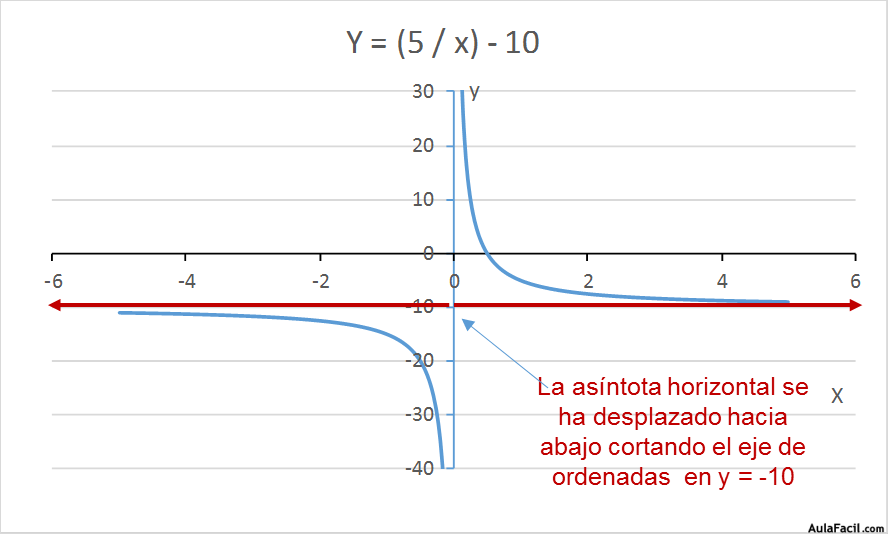
2.- Funciones racionales del tipo y = k / (x + a) (siendo a un número real)

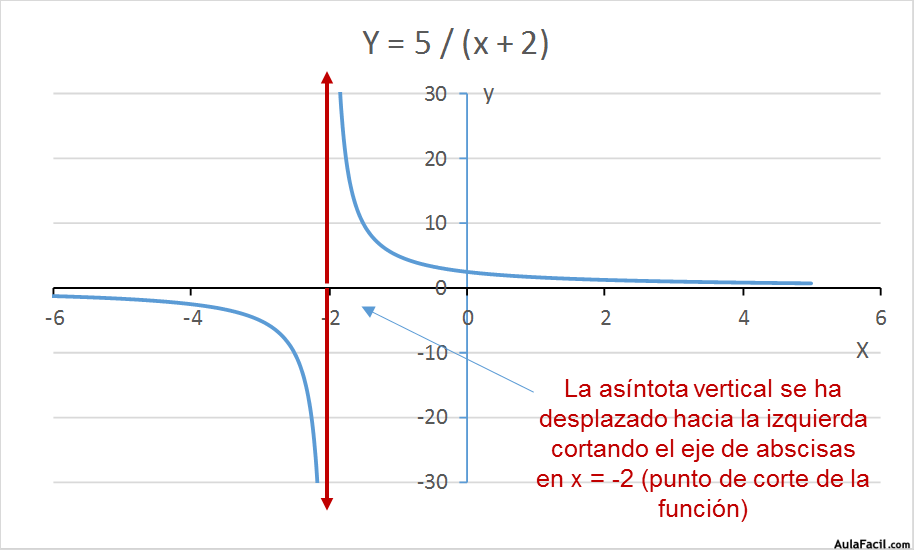
La gráfica de esta función es similar a la de la función de proporcionalidad inversa, simplemente se habrá desplazado hacia la izquierda o hacia la derecha dependiendo de que el número “a” sea positivo o negativo.

y = 7 / (x + 2)

y = 7 / (x - 3)

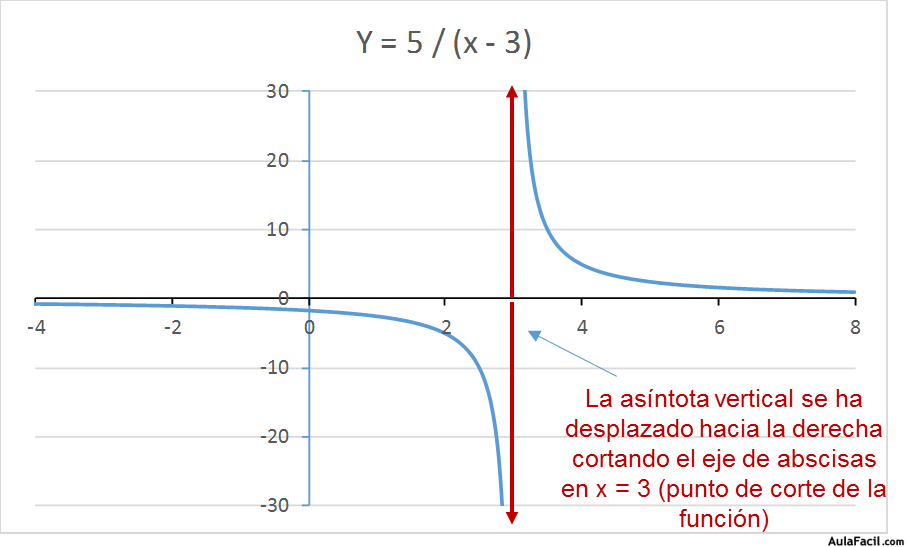
b) Funciones racionales del tipo y = (ax + b) / (cx + d)

y = (3x + 4) / (2x - 6)

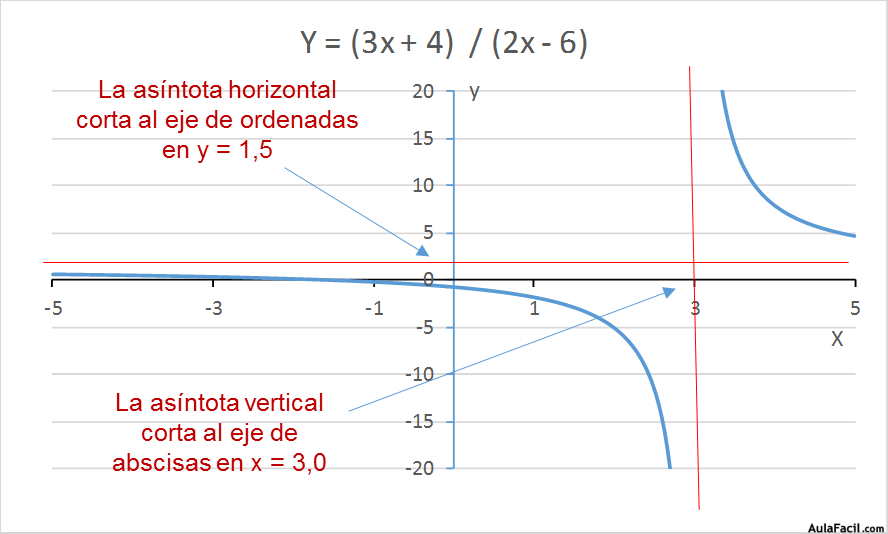
Vemos que su gráfica también es una hipérbole, si bien sus asíntotas se han desplazado.

La asíntota horizontal corta al eje de ordenadas en y = 1,5.

Para calcularlo dividimos el numerador entre el denominador:

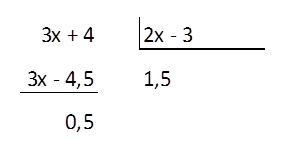
La función la podemos escribir:

y = (3x + 4) / (2x - 3) = 1,5 + (0,5 /(2x - 3))

Calculamos el valor al que tiende y cuando x tiende a +/- ∞

y = 1,5 + (0,5 /(2x - 3)) = 1,5 + (0,5 /(+/- ∞ - 3)) = 1,5 + 0 = 1,5

La asíntota vertical corta al eje de abscisas en x = 3,0.

Lo podemos calcular viendo el valor que hace 0 el denominador (punto de corte de la función):

(2x - 6) = 0

X = 6 / 2 = 3,0

2.- Funciones radicales

Una función radical es aquella en la que la variable independiente x figura dentro de un radical.

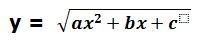
Dentro de esta tipología de funciones vamos a analizar las funciones del tipo

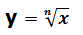
Por ejemplo:

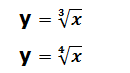
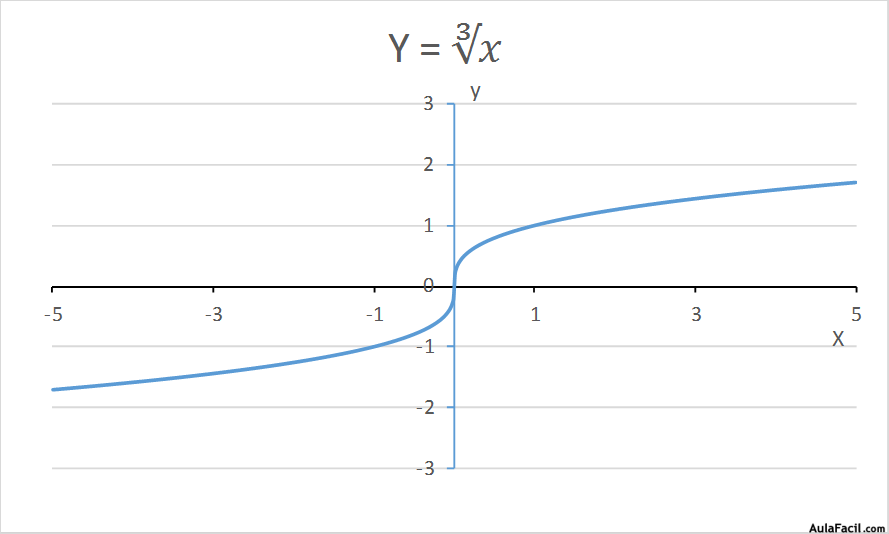
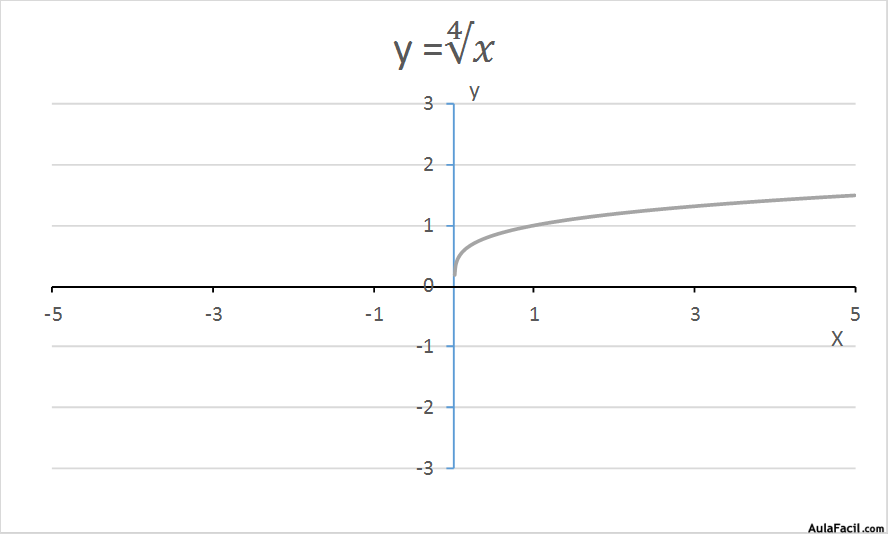
Características de estas funciones:

Dominio: el dominio de estas funciones con radical par va de 0 (excluido) hasta ∞; estas funciones no están definidas para valores de x negativos o 0 (no existe una raíz par de un número negativo o cero). Mientras que el dominio de estas funciones con radical impar es -∞, ∞

Recorrido: su recorrido, con independencia del exponente, es +/- ∞

Punto de corte: las funciones radicales con exponente impar son continuas mientras que las que tienen exponente par tienen un punto de corte en x = 0.

Simetría: las funciones radicales con exponente impar son simétricas respecto al origen de coordenadas. Las funciones exponenciales son funciones en las que la variable independiente x figura en el exponente, mientras que la base es un número real positivo. Por ejemplo:

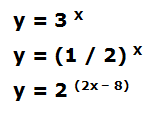
Estas funciones tienen por dominio el conjunto de los números reales, mientras su recorrido es el intervalo (0, ∞), ya que la exigencia de que la base sea un número real positivo hace que la potencia siempre será positiva.

Vamos a distinguir 2 supuestos:

a) Base > 1

Por ejemplo:

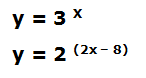
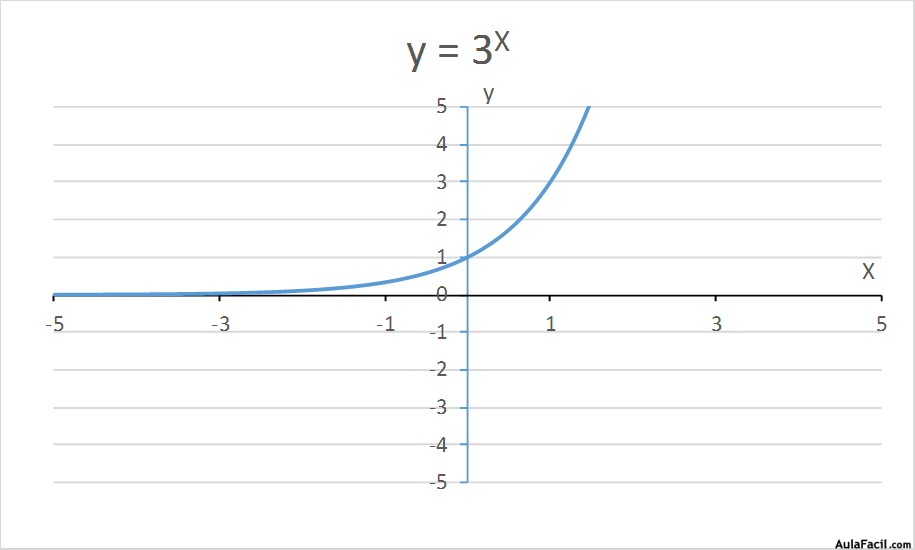
Su representación gráfica es una línea continua monótona creciente, asintótica a y = 0 cuando x tiende a -∞.

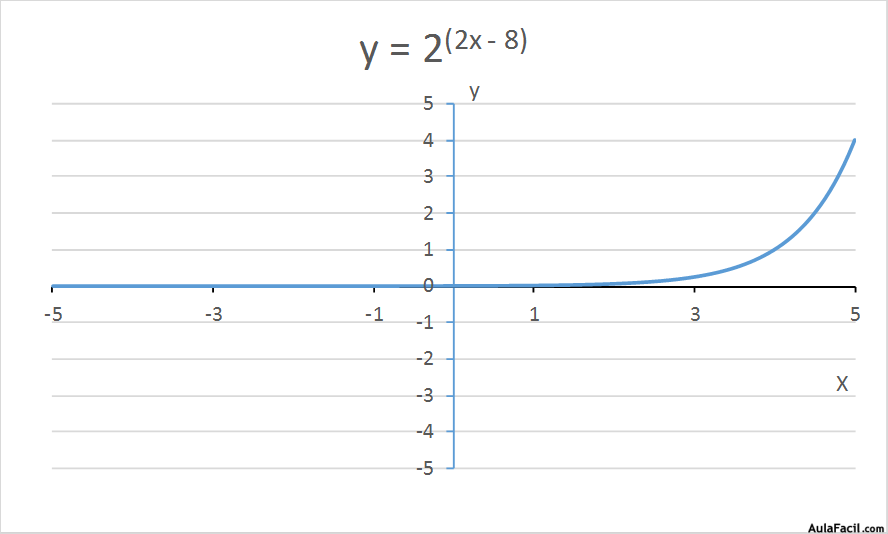
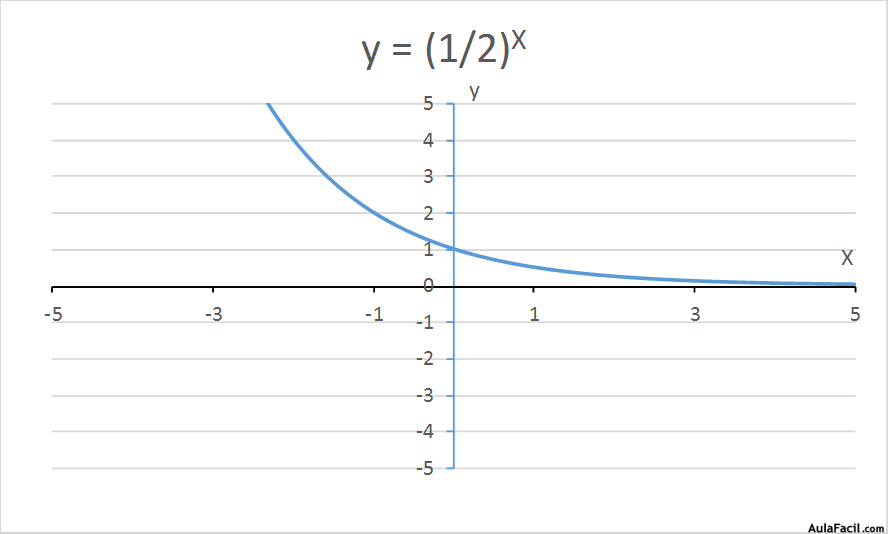
b) 0 > Base > 1

Por ejemplo:

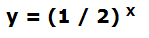
Su representación gráfica es una línea continua monótona decreciente, asintótica a y = 0 cuando x tiende a ∞.