Puntos de corte de los ejes de abscisas y ordenadas
Puntos de corte de los ejes de abscisas y ordenadas
1.- La función corta el eje de abscisas en aquellos valores de la variable independiente “x” que hacen 0 el valor de la variable dependiente “y”. Para calcular estos valores igualamos a cero la función y hallamos las raíces.
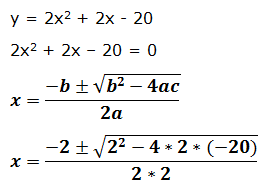
Las raíces son:
X1 = 2,70
X2 = -3,70
2.- La función corta el eje de ordenadas en el valor que toma la variable dependiente “y” cuando la variable independiente “x” vale 0.
Dada la función típica cuadrática: y = ax2 + bx + c
y = a * 02 + b * 0 + c = c
Por lo tanto, la función cuadrática corta al eje de ordenadas precisamente en el valor del término independiente “c”.
y = 2x2 + 2x – 20
Si x = 0, entonces y = -20
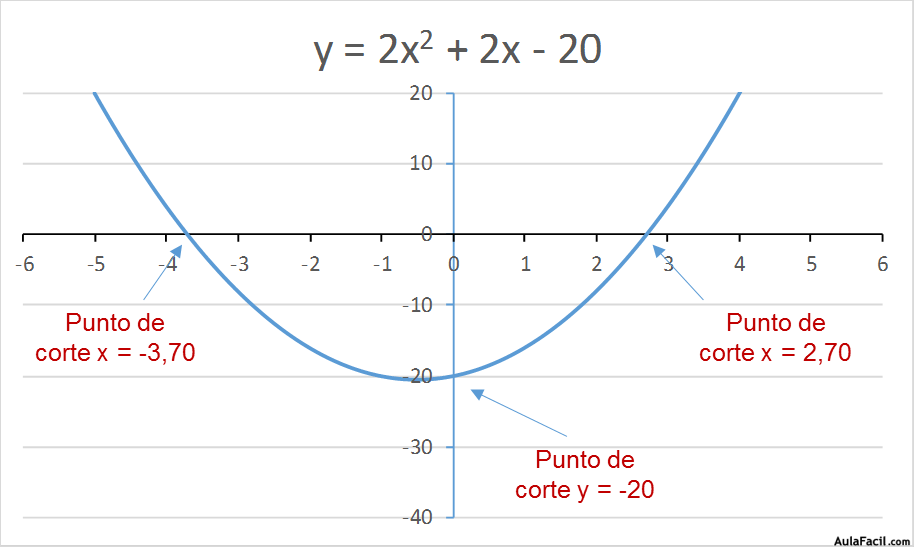
Veamos otro ejemplo:
y = 5x2 - 10x – 25
1.- Calculamos el punto (s) de corte en el eje de abscisas:
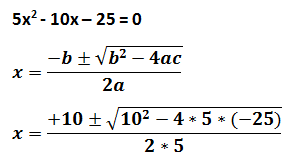
Las raíces son:
X1 = 3,45
X2 = -1,45
2.- Calculamos el punto de corte en el eje de ordenadas:
Si x = 0 entonces:
y = -25
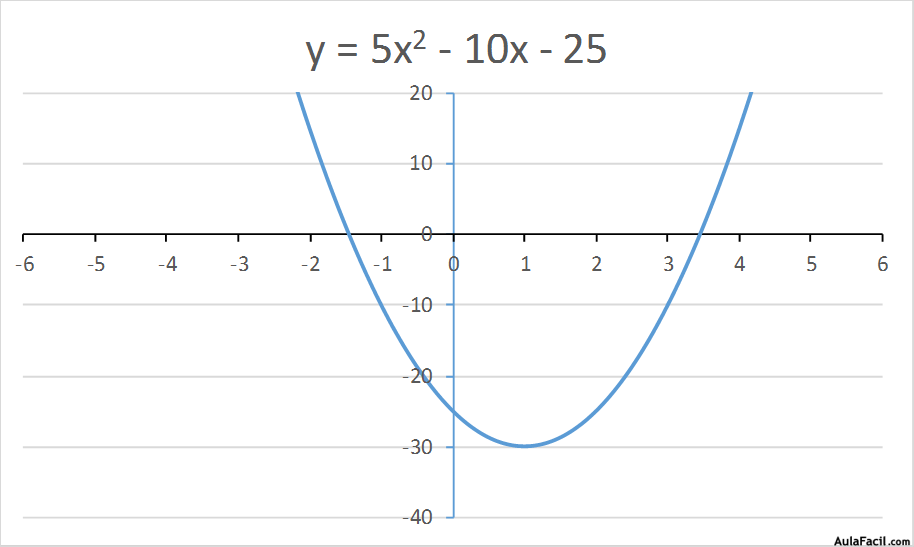
La función cuadrática siempre corta al eje de ordenadas pero puede ocurrir que la función no corte el eje de abscisas.
De hecho podemos ver que a estas ecuaciones:
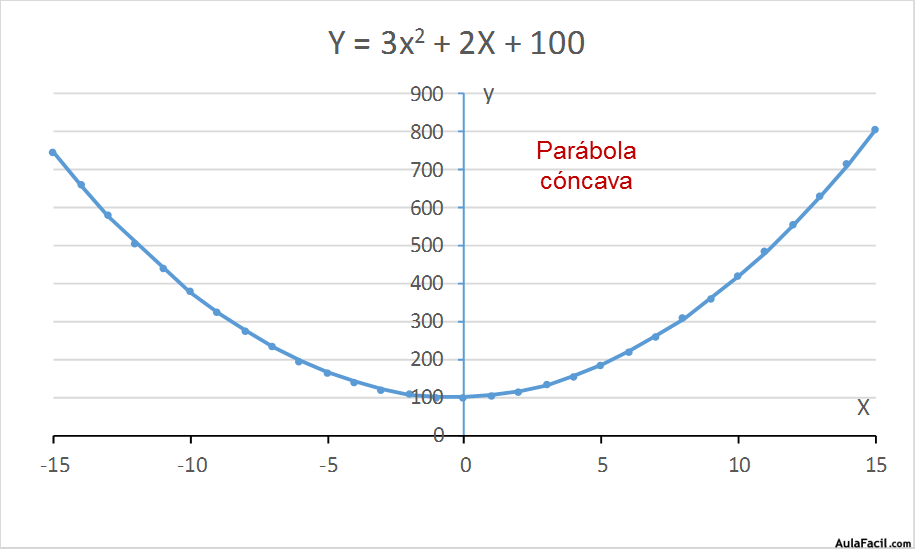
3x2 + 2x + 100 = 0
-5x2 + 4x – 50 = 0
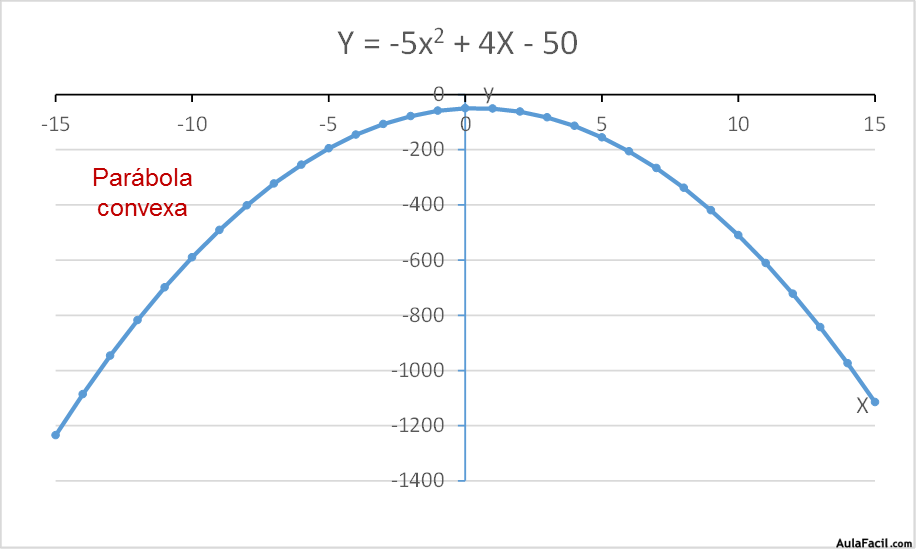
No se le pueden calcular sus raíces.
Mínimo y máximo
Si la función tiene forma de parábola cóncava tiene un mínimo absoluto y si tiene forma de parábola convexa tiene un máximo absoluto.
Vamos a utilizar como ejemplo la función que vimos anteriormente:
y = 5x2 - 10x – 25
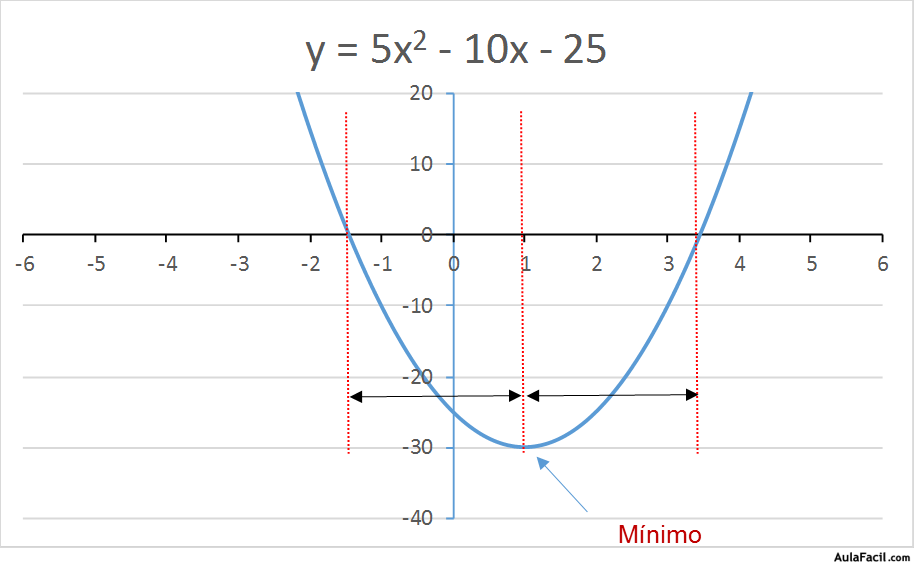
Podemos ver que el vértice inferior (mínimo) corresponde a un valor de la “x” situando en un punto intermedio entre las 2 raíces x1 y x2 (puntos de corte del eje de abscisas).
Luego este valor x se puede calcular como punto intermedio entre las 2 raíces:
x = (x1 + x2) / 2
Sustituyendo estas raíces por sus definiciones:
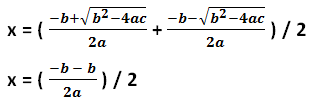
El valor de la variable x a la que le corresponde el mínimo (máximo) es:
x = -b / 2a
En la función anterior:
x = +10 / (2*5) = 1
El valor de la y correspondiente a este valor de la x:
y = 5x2 - 10x – 25
y = 5 * (1)2 – 10 * 1 – 25 = -30
Las coordenadas de este mínimo de la parábola es (1, -30)
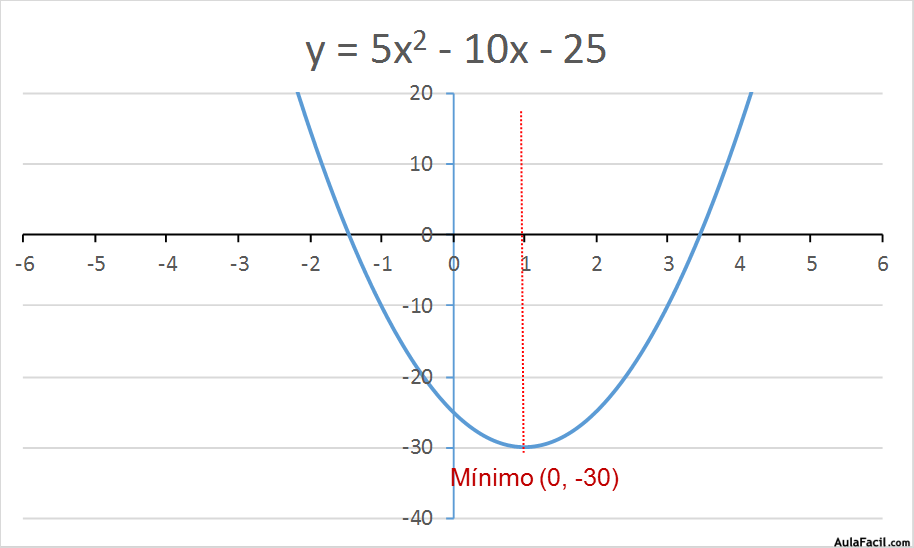
Por otra parte podemos ver que la gráfica de esta función es simétrica respecto a un eje que pasa por este vértice.
Veamos otro ejemplo:
y = -2x2 + 8x + 20
El valor de la variable x a la que le corresponde el máximo (parábola convexa) se calcula:
x = -b / 2a = -8 / (2 * (-2)) = 2
El valor de la y:
y = -2x2 + 8x + 20 = -2 * (2)2 + 8 * (2) + 20 = 28
Las coordenadas de este máximo de la parábola es (2, 28)
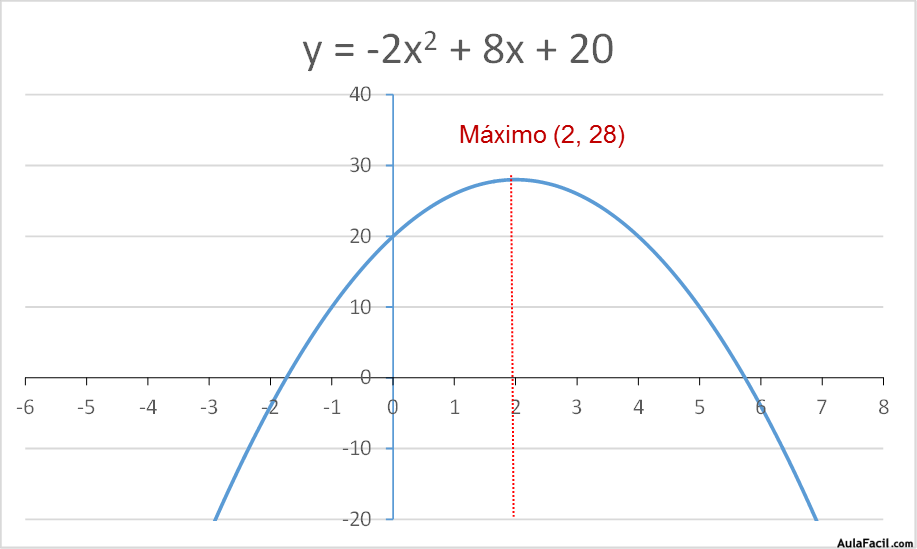
Características de estas funciones:
1.- Dominio: el conjunto de números reales R (- ∞; ∞).
2.- Función continua en todo su dominio.
3.- Recorrido: Si la función es cóncava, el recorrido es (∞, mínimo); si la función es convexa, el recorrido es (-∞, máximo).
4.- Simétrica respecto al eje que pasa por el vértice (máximo / mínimo).
Funciones potenciales (tipo: y = axn)
Vamos a distinguir si el exponente es positivo o si es negativo.
1.- Funciones potenciales con exponente positivo
Ejemplos:
y=2x2
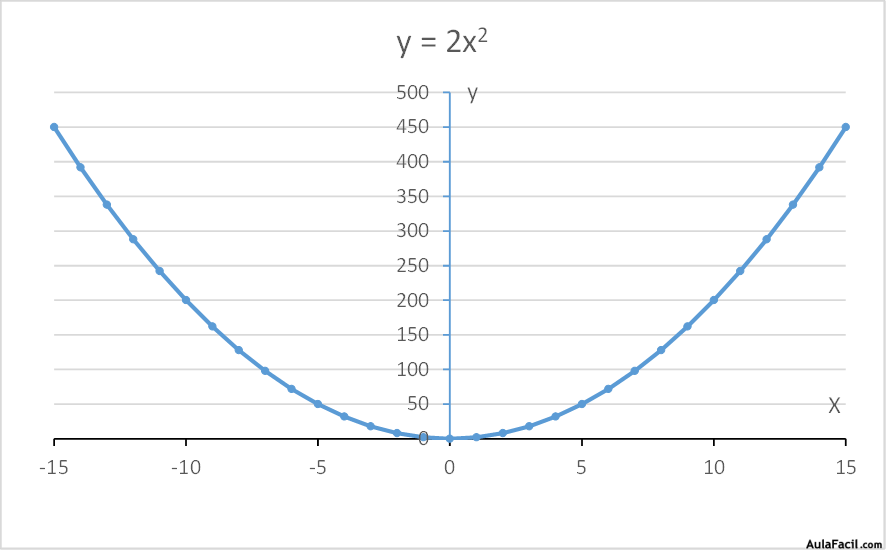
y=5x3
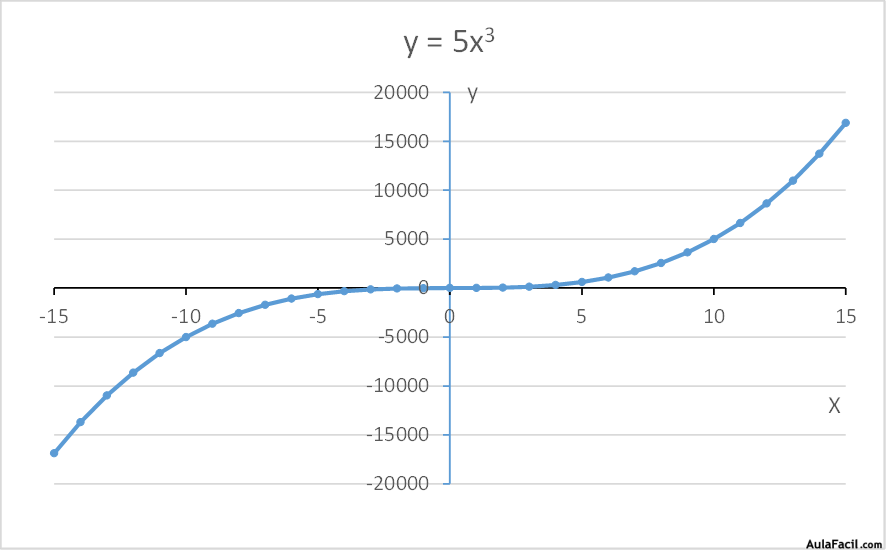
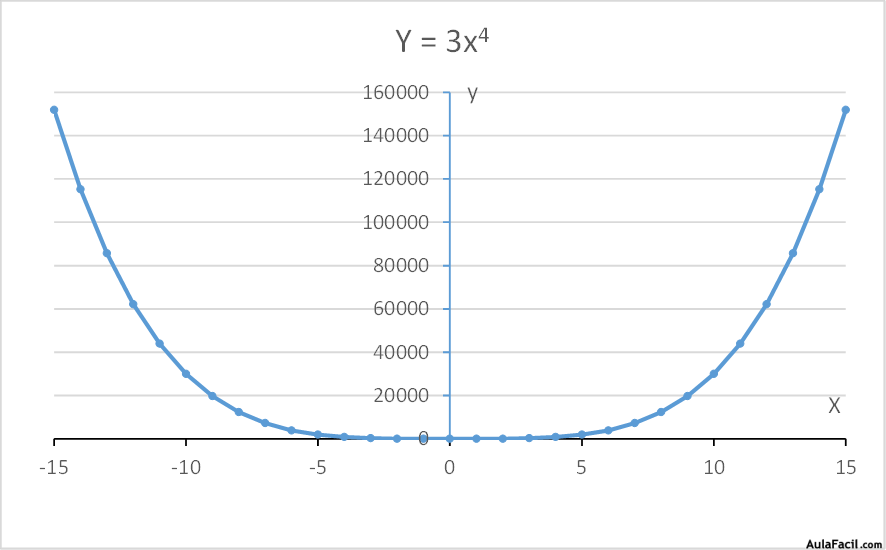
y=3x4
y=7x5
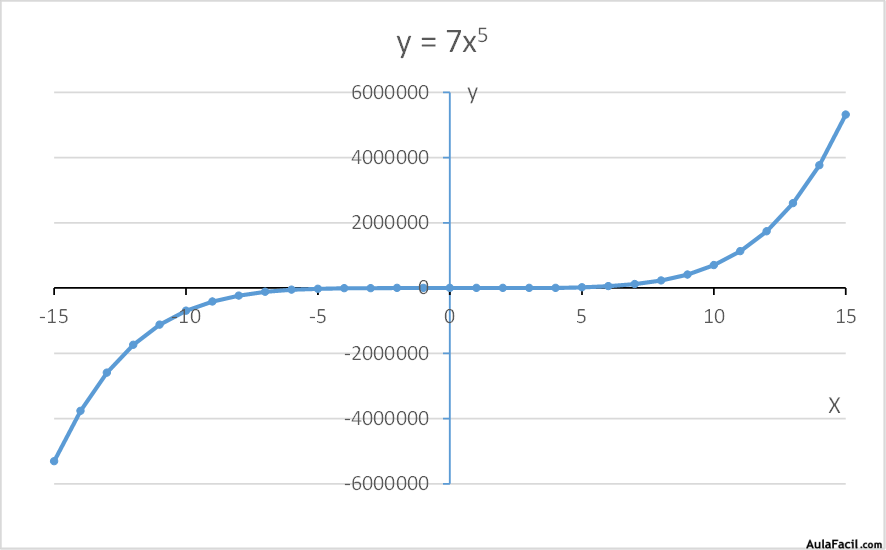
Vemos que la forma de estas funciones varía en función del exponente: si es par tiene forma parabólica, si es impar tiene forma de tipo espiral.
2.- Funciones potenciales con exponente negativo
Ejemplos:
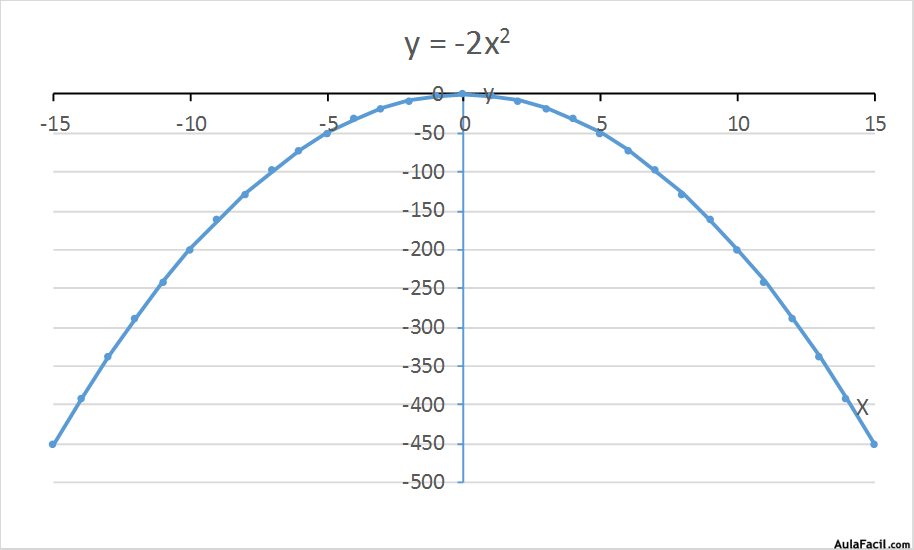
y = -2x2
y = -5x3
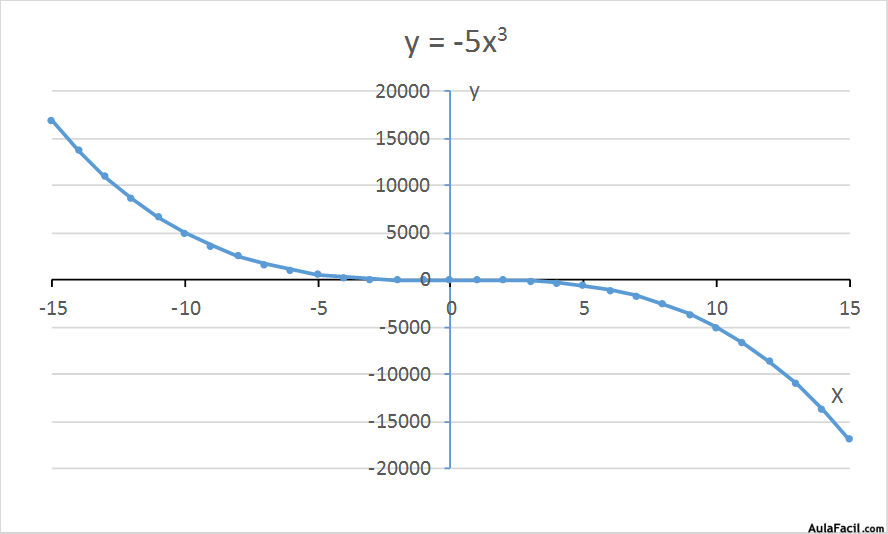
La forma de estas funciones es igual que las del punto anterior pero invertidas.
En función del signo y del exponente distinguimos:
- Término positivo y exponente par: parábola cóncava.
- Término negativo y exponente par: parábola convexa.
- Término positivo y exponente impar: espiral creciente.
- Término negativo y exponente impar: espiral decreciente.
1.- Dominio: el conjunto de números reales R (- ∞; ∞)
2.- Función continua en todo su dominio.
3.- Recorrido: si el exponente es par su recorrido depende del signo del término a: si el término es positivo (∞, mínimo); si el término es negativo (-∞, máximo). Si el exponente es impar su recorrido es (-∞,∞).
4.- Si el exponente es par la función es simétrica respecto al eje de ordenadas. Si el exponente es impar la función es simétrica respecto al origen de coordenadas.


