Composiciones de funciones y operaciones algebraicas
Composición de funciones
Se llama composición de funciones al proceso por el cual a partir de 2 funciones, la variable dependiente de la 1ª función pasa a ser la variable independiente de la 2ª función.
y = 3x + 2
z = x2 / 3
La composición de estas 2 funciones:
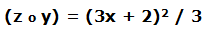
Hemos sustituido la variable independiente en la función z por la función y.
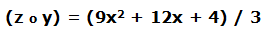
Veamos una tabla con una muestra de valores de esta composición de funciones:
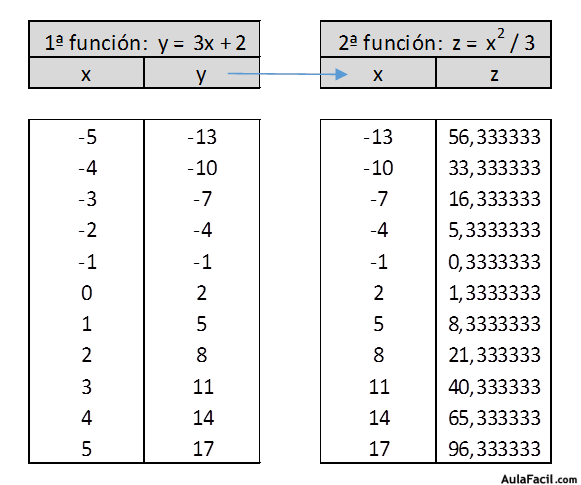
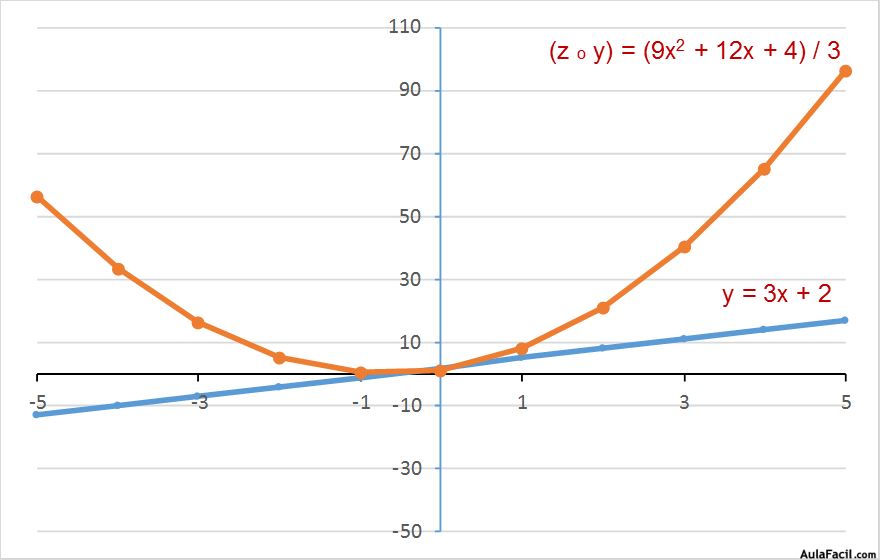
Puede haber composiciones de 3 o más funciones: la variable dependiente de la 1ª función pasa a ser la variable independiente de la 2ª función; y la variable dependiente de la 2ª función pasa a ser la variable independiente de la 3ª función…
Funciones inversas
Una función z es inversa de otra función y cuando al componer las 2 funciones se obtiene la función identidad.
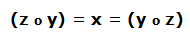
Vemos que la relación de inversión se cumple en las 2 direcciones: componiendo la 2ª sobre la 1ª y componiendo la 1ª sobre la 2ª.
y = 2x
z = x / 2
La composición de estas 2 funciones:
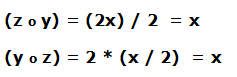
La relación inversa se expresa:
z = y-1
y = z-1
Las gráficas de las funciones inversas son simétricas respecto al origen de coordenadas y respecto a la bisectriz del cuadrante superior-derecho e inferior-izquierdo.
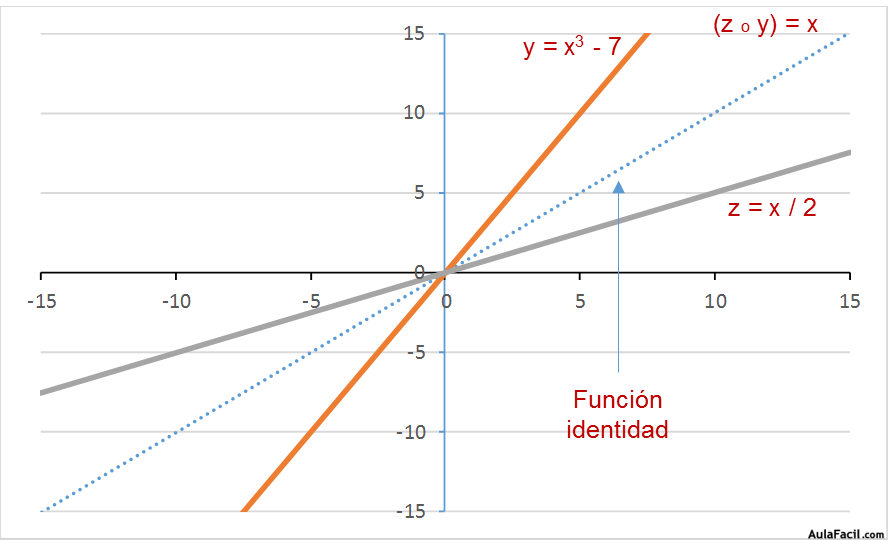
Vamos a ver como a partir de una función dada (y) podemos calcular su función inversa:
Ejemplo:
y = x3 – 7
Intercambiamos las variables:
x = y3 – 7
Despejamos la variable y:
y3 = x + 7
La función inversa es:
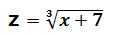
Esta es la función inversa de la primera
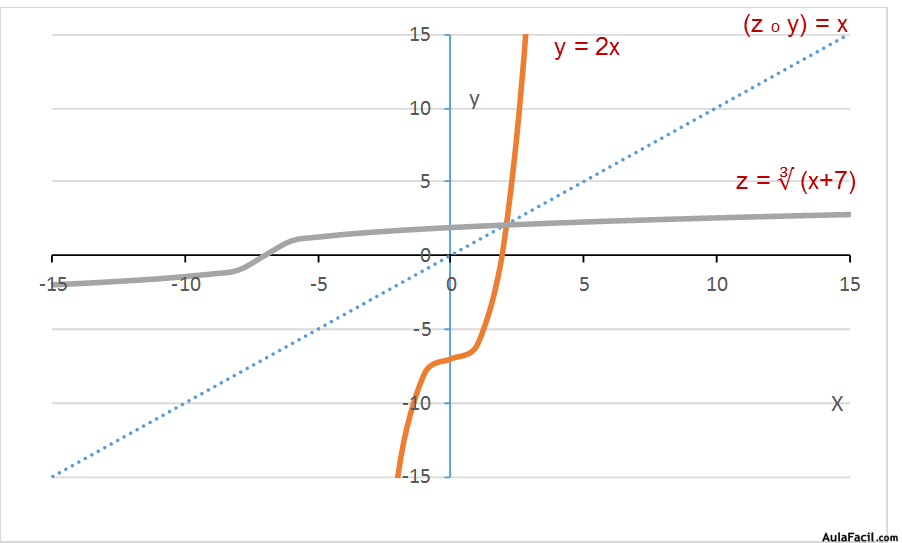
Un ejemplo de funciones inversas son las funciones logarítmicas y las funciones exponenciales.
Ejemplo:
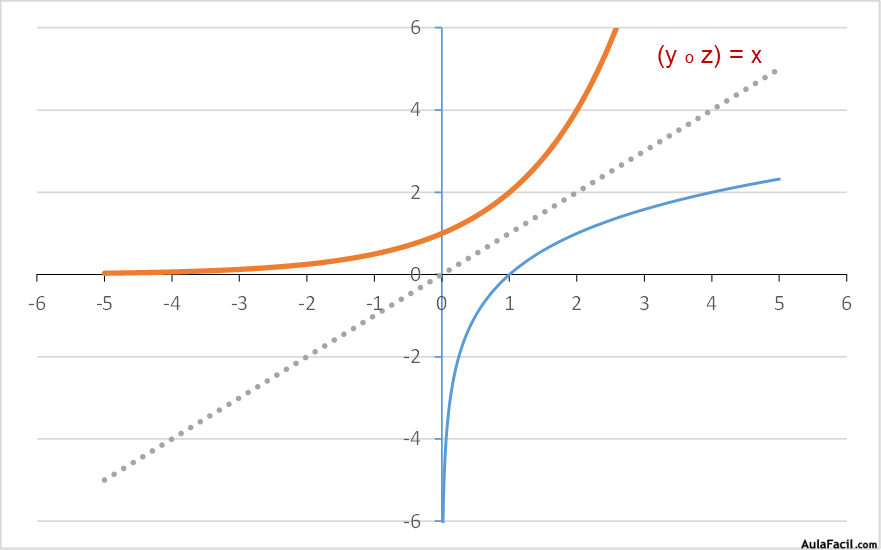
Vamos a representar las funciones:
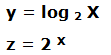
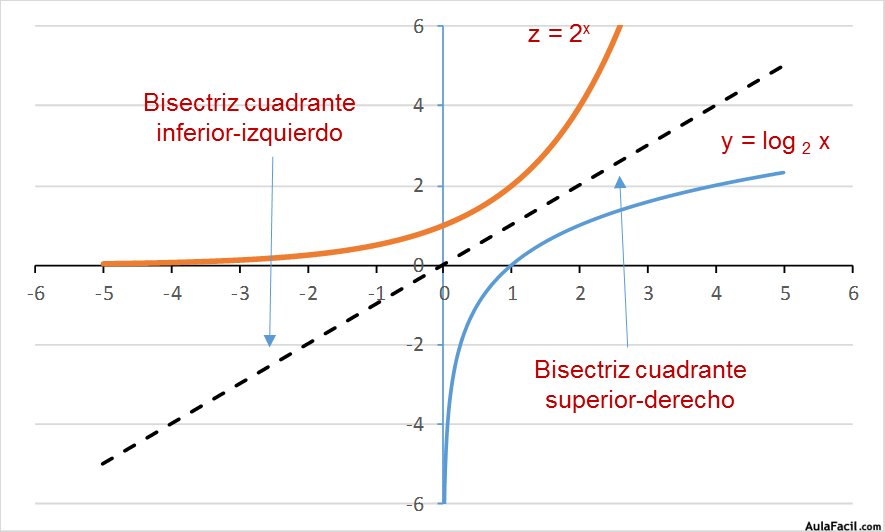
Vemos que ambas funciones son simétricas respecto al origen de coordenadas y respecto a la bisectriz del cuadrante superior-derecho e inferior-izquierdo.
Ahora vamos a calcular la composición de funciones:
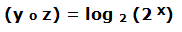
Podemos ver que obtenemos la función identidad; lo mismo ocurre si componemos la segunda de la primera.
Operaciones con funciones
Las funciones se pueden sumar, restar, multiplicar o dividir.
La suma de 2 funciones: (p + q) (x) = p(x) + q(x)
La resta de 2 funciones: (p - q) (x) = p(x) - q(x)
La multiplicación de 2 funciones: (p * q) (x) = p(x) * q(x)
La división de 2 funciones: (p / q) (x) = p(x) / q(x)
Veamos un ejemplo con las funciones:
y = 3x + 5
z = 2x -3
Suma: y + z = (3x + 5) + (2x -3) = 5x + 2
Resta: y – z = (3x + 5) - (2x -3) = x + 8
Multiplicación: y * z = (3x + 5) * (2x -3) = 6x2 + x - 15
División: y / z = (3x + 5) / (2x -3)


