Sistema de ecuaciones lineales
Llamamos sistema de ecuaciones lineales a un conjunto de ecuaciones lineales.
La ecuación lineal tiene la forma de un polinomio de primer grado: las incógnitas no están elevadas a ningún exponente, ni van multiplicadas entre sí, ni figuran en el denominador.
Ejemplo:
3x – 4y = 5 – 3z
Hemos visto ya que una ecuación lineal con 2 incógnitas representa una recta en el plano.
Una ecuación lineal con 3 incógnitas representa un plano en el espacio.
Un sistema de ecuaciones lineales puede estar integrado por 2, 3, 4... ecuaciones. Veamos algunos ejemplos:
a) Sistema de 2 ecuaciones con 2 incógnitas:
3x + 2y = 7
X – 4y = 0
b) Sistema de 3 ecuaciones con 3 incógnitas:
2x – 3y + 4z = 5
x – y + 2z = 7
2x – 5x + 4z = 3
Como forma general un sistema formado por “m” ecuaciones con “n” incógnitas quedaría representado.

Siendo las “aij” los coeficientes, las “xi” las incógnitas y las “bj” los términos independientes.
Un sistema de ecuaciones lineales se puede representar en forma matricial:

De las tres matrices anteriores, la primera se denomina matriz de coeficientes, la segunda matriz de incógnitas y la tercera matriz de términos independientes.
Vamos a representar un sistema de ecuaciones lineales de forma matricial:
2x + 3y – 2z = 5
3x – z = 4
x – 3y = 8
Su representación matricial sería:
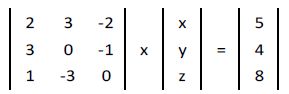
Resolver un sistema de ecuaciones lineales es hallar aquellos valores de las incógnitas que son soluciones a la vez de todas las ecuaciones del sistema.
Los sistemas pueden ser compatibles e incompatibles:
- Sistema compatible es aquel que tiene soluciones en el conjunto de los números reales R. Si tiene una única solución se denomina sistema compatible determinado y si tiene infinitas soluciones se denomina sistema compatible indeterminado.
- Sistema incompatible es aquel que no tiene soluciones en el conjunto de los números reales R
Dos sistemas que tengan las mismas soluciones se dice que son sistemas equivalentes.


