Ejercicios
En esta y en las siguientes lecciones vamos a ver cómo se resuelven los siguientes ejercicios:
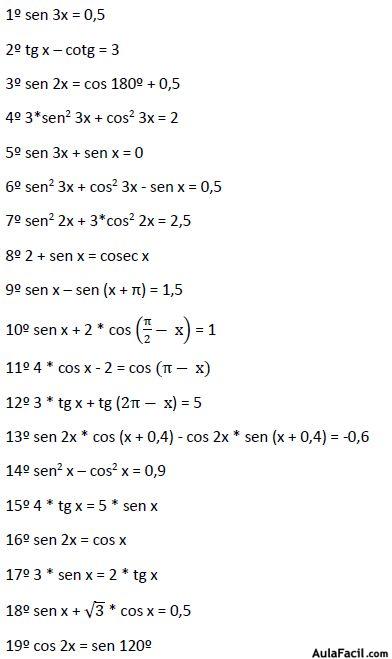
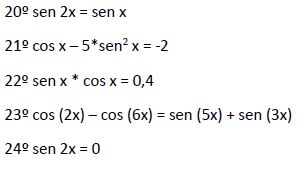
1er ejemplo
sen 3x = 0,5
Luego “3x” será igual al arcoseno de 0,5:
3x = arcsen (0,5)
3x = 0,5236
x = 0,5236 / 3
x1 = 0,1745 (expresado en radianes) / 10º 00’ 00’’ (expresado en grados)
Comprobamos que la solución x1 = 0,1745 cumple la igualdad de la ecuación inicial.
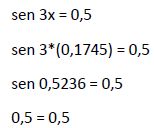
Hemos visto que la función seno tiene un periodo de 2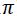
(360º / 6,2832 radianes); luego también será solución de la ecuación:
3x = 0,5236 + 6,2832
x = 6,8068 / 3
x1 = 2,2689 (expresado en radianes) / 130º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
3x = 0,5236 + (2 * 6,2832)
2º ejemplo
tg x – cotg x = 3
Realizamos aquellas transformaciones que nos permitan trabajar con una sola función trigonométrica. Aplicamos la ley de trigonometría que dice:
Resolvemos esta ecuación aplicando el sistema de resolución de ecuaciones de segundo grado con una incógnita:
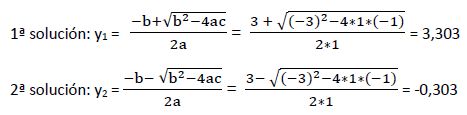
Procedemos a calcular la variable original:
1ª solución: (y1 = 3,303)
tg x = y1
tg x = 3,303
x = arctg (3,303)
x1 = 1,277 (expresado en radianes) / 73º 09’ 18’’ (expresado en grados)
Comprobamos si esta solución cumple la igualdad en la ecuación original:
tg x – cotg x= 3
tg 1,277 – cotg 1,277 = 3
3,303 – 0,303 = 3
3 = 3
Por lo tanto la solución calculada (x1 = 1,277) cumple la igualdad de la ecuación inicial.
2ª solución: (y2 = -0,303)
tg x = y2
tg x = -0,303
x = arctg (-0,303)
x2 = -0,294 (expresado en radianes) / -17º 09’ 18’’ (expresado en grados) chequear.
Comprobamos si esta solución cumple la igualdad en la ecuación original:
tg x – cotg x = 3
tg -0,294 – cotg -0,294 = 3
-0,303 – (-3,303) = 3
3 = 3
Por lo tanto la solución calculada (x2 = -0,294) cumple la igualdad de la ecuación inicial
La función tangente tiene un periodo de π (180º / 3,1416 radianes); luego también serán soluciones de la ecuación:
1ª solución:
x1 = 1,277 + 3,1416 = 4,418 (expresado en radianes) / 253º 09’ 18’’ (expresado en grados)
2ª solución:
x2 = -0,294 + 3,1416 = 2,848 (expresado en radianes) / 163º 09’ 18’’ (expresado en grados)
La solución se irá repitiendo cada 180º.
x1 = 1,277 + (2 * 3,1416)
x2 = -0,294 + (2 * 3,1416)
3er ejemplo
sen 2x = cos 180º + 0,5
sen 2x = -1 + 0,5
sen 2x = -0,5
2x = arcsen (-0,5)
2x = -0,5236
x1 = -0,5236 / 2 = -0,2618 (expresado en radianes) / -15º 00’ 00’’ (expresado en grados)
Comprobamos si esta solución (x1 = -0,2618) cumple la igualdad en la ecuación original:
sen 2x = cos 180º + 0,5
sen (2*(-0,2618)) = cos 180º + 0,5
sen -0,5236 = cos 180º + 0,5
-0,5 = -1 + 0,5
-0,5 = -0,5
Por lo tanto la solución calculada (x1 = -0,2618) cumple la igualdad de la ecuación inicial
La función seno tiene un periodo de 2π (360º / 6,2832 radianes); luego también será solución de la ecuación:
2x = -0,5236 + 6,2832
x = 5,7596 / 2
x1 = 2,9798 (expresado en radianes) / 165º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
2x = -0,5236 + (2 * 6,2832)
4º ejemplo
Comprobamos si esta solución (x1 = 0,2618) cumple la igualdad en la ecuación original:
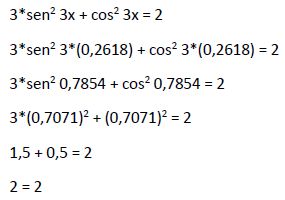
Por lo tanto la solución calculada (x1 = 0,2618) cumple la igualdad de la ecuación inicial, siendo por tanto solución de la ecuación inicial.
b) Analizamos la segunda solución: sen 3x = -0,7071
3x = arcsen (-0,7071)
3x = -0,78546
x1 = -0,2618 (expresado en radianes) / -15º 00’ 00’ (expresado en grados)
Comprobamos si esta solución (x2 = -0,2618) cumple la igualdad en la ecuación original:
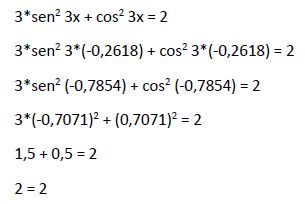
Por lo tanto la solución calculada (x2 = -0,2618) cumple la igualdad de la ecuación inicial, siendo por tanto solución de la ecuación inicial.
La función seno tiene un periodo de 2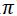
(360º / 6,2832 radianes); luego también será solución de la ecuación:
1ª solución:
3x = 0,78546 + 6,2832
x1 = 2,3562 (expresado en radianes) / 135º 00’ 00’’ (expresado en grados)
2ª solución:
3x = -0,78546 + 6,2832
x2 = 1,8326 (expresado en radianes) / 105º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 180º.
3x1 = 0,78546 + (2 * 3,1416)
3x2 = -0,78546 + (2 * 3,1416)
5º ejemplo
sen 3x + sen x = 0
Aplicamos la relación trigonométrica que dice:
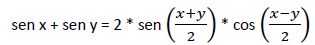
La ecuación quedaría:
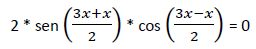
Para que el producto sea igual a 0 alguno de los factores tiene que ser 0.
a) Igualamos el primer factor:
Comprobamos si esta solución (x1 = 0) cumple la igualdad en la ecuación original:
sen 3x + sen x = 0
sen 0 + sen 0 = 0
0 + 0 = 0
Por lo tanto la solución calculada (x1 = 0) cumple la igualdad de la ecuación inicial, siendo por tanto solución de la ecuación inicial.
b) Igualamos el segundo factor:
Comprobamos si esta solución (x2 = 1,5708) cumple la igualdad en la ecuación original:
sen 3x + sen x = 0
sen (3 * 1,5708) + sen 1,5708 = 0
sen 4,7124 + sen 1,5708 = 0
-1 + 1 = 0
0 = 0
Por lo tanto la solución calculada (x2 = 1,5708) cumple la igualdad de la ecuación inicial, siendo por tanto solución de la ecuación inicial.
La funciones seno y coseno tienen un periodo de 2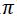
(360º / 6,2832 radianes); luego también serán soluciones de la ecuación:
1ª solución:
2x = 0 + 6,2832
x1 = 3,141 (expresado en radianes) / 180º 00’ 00’’ (expresado en grados)
2ª solución:
x2 = 1,5708 + 6,2832
x2 = 7,8540 (expresado en radianes) / 450º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
2x1 = 0 + (2 * 6,2832)
x2 = 1,5708 + (2 * 6,2832)
6º ejemplo
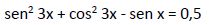
Aplicamos la relación trigonométrica que dice:
Comprobamos si esta solución (x1 = 0,5236) cumple la igualdad en la ecuación original:
Por lo tanto la solución calculada (x1 = 0,5236) cumple la igualdad de la ecuación inicial, siendo por tanto solución de la ecuación inicial.
La función seno tiene un periodo de 2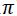
(360º / 6,2832 radianes); luego también será solución de la ecuación:
1ª solución:
x = 0,5236 + 6,2832
x1 = 6,8068 (expresado en radianes) / 390º 0’ 0’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x1 = 0,5236 + (2 * 6,2832)
