Ejercicios (Continuación)
17º ejemplo

Comprobamos si esta solución x1 = 0,8411 cumple la igualdad en la ecuación inicial:
3 * sen x = 2 * tg x
3 * sen 0,8411 = 2 * tg 0,8411
3 * 0,7453 = 2 * 1,1180
2,2361 = 2,2361
Por lo tanto la solución x1 = 0,8411 es solución válida de la ecuación inicial.
La función coseno tiene un periodo de 2π (360º / 6,2832 radianes); luego también será solución de la ecuación:
x1 = 0,8411 + 6,2832
x1 = 7,1243 (expresado en radianes) / 408º 11’ 23’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x1 = 0,8411 + (2 * 6,2832)
18º ejemplo
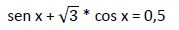
Comenzamos a operar buscando simplificar la ecuación inicial:
a) Dividimos ambos miembros de la ecuación entre 2:
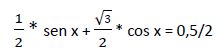
b) Aplicamos la siguiente relación trigonométrica:
sen (x + y) = sen x * cos y + cos x * sen y
c) En la tabla de valores de las funciones trigonométricas vemos que:
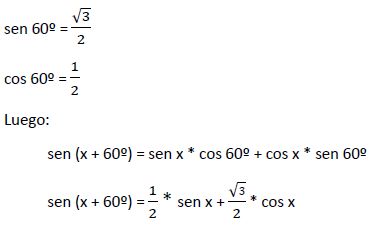
Sustituyendo en la ecuación inicial quedaría:
sen (x + 60º) = 0,25
x + 60º = arcsen (0,25)
x + 60º = 0,2527
Como la solución la tenemos expresada en radianes convertimos 60º en radianes:
60º = 1,0472 radianes
Por lo tanto
x + 1,0472 = 0,2527
x1 = -0,7945 (expresado en radianes) / -45º 31’ 21’’ (expresado en grados)
Comprobamos si esta solución x1 = -0,7945 cumple la igualdad en la ecuación inicial:
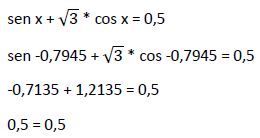
Por lo tanto la solución x1 = -0,7945 es solución válida de la ecuación inicial.
La función seno tiene un periodo de 2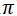 (360º / 6,2832 radianes); luego también será solución de la ecuación:
(360º / 6,2832 radianes); luego también será solución de la ecuación:
x1 = -0,7945 + 6,2832
x1 = 5,4887 (expresado en radianes) / 314º 28’ 39’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x1 = -0,7945 + (2 * 6,2832)
19º ejemplo
cos 2x = sen 120º
Operamos:
cos 2x = 0,8660
2x = arccos (0,8660)
2x = 0,5236
x1 = 0,2618 (expresado en radianes) / 15º 00’ 00’’ (expresado en grados)
Comprobamos si esta solución x1 = 0,2618 cumple la igualdad en la ecuación inicial:
cos 2x = sen 120º
cos 2*0,2618 = 0,8660
0,8660 = 0,8660
Por lo tanto la solución x1 = 0,2618 es solución válida de la ecuación inicial.
La función coseno tiene un periodo de 2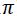 (360º / 6,2832 radianes); luego también será solución de la ecuación:
(360º / 6,2832 radianes); luego también será solución de la ecuación:
1ª solución:
x1 = 0,2618 + 6,2832
x1 = 6,5450 (expresado en radianes) / 375º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x1 = 0,2618 + (2 * 6,2832)
20º ejemplo
sen 2x = sen x
Expresamos todos los términos de la ecuación con el mismo ángulo:
sen 2x = 2 * sen x * cos x
Luego la ecuación quedaría:
2 * sen x * cos x = sen x
Operamos:
2 * sen x * cos x - sen x = 0
sen x * (2 * cos x -1) = 0
Si el producto es igual a cero esta igualdad se cumple cuando cualquiera de los factores es igual a 0. Luego igualamos cada factor a cero:
a) sen x = 0
x = arcsen (0)
x1 = 0 (expresado en radianes) / 0º 00’ 00’’ (expresado en grados)
b) (2 * cos x -1) = 0
2 * cos x = 1
cos x = 1 / 2
x = arccos (0,5)
x2 = 1,0472 (expresado en radianes) / 60º 00’ 00’’ (expresado en grados)
Comprobamos si estas soluciones cumplen la igualdad en la ecuación inicial:
a) x1 = 0
sen 2x = sen x
sen (2*0) = sen 0
sen 0 = sen 0
0 = 0
Por lo tanto la solución x1 = 0 lo es de la ecuación inicial
b) x2 = 1,0472
sen 2x = sen x
sen (2*1,0472) = sen 1,0472
sen 2,0944 = sen 1,0472
0,8660 = 0,8660
Por lo tanto la solución x2 = 1,0472 también lo es de la ecuación inicial
La función seno y coseno tienen un periodo de 2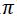 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
1ª solución
x1 = 0 + 6,2832
x1 = 6,2832 (expresado en radianes) / 360º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x1 = 0 + (2 * 6,2832)
2ª solución
x2 = 1,0472 + 6,2832
x2 = 7,3304 (expresado en radianes) / 420º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x2 = 1,0472 + (2 * 6,2832)
21º ejemplo

Resolvemos esta ecuación aplicando el sistema de resolución de ecuaciones de segundo grado con una incógnita:
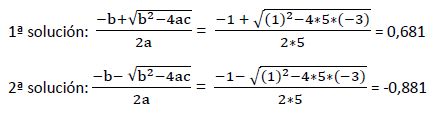
Procedemos a calcular la variable original:
1ª solución: (y1 = 0,681)
y = cos x
0,681 = cos x
x = arccos (0,681)
x1 = 0,8216 (expresado en radianes); 47º 04’ 34’’ (expresado en grados)
Comprobamos si esta solución x1 = 0,8216 cumple la igualdad en la ecuación inicial:
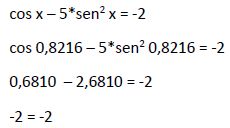
Por lo tanto la solución x1 = 0,8216 es solución de la ecuación inicial.
2ª solución: (y2 = -0,881)
y = cos x
-0,881 = cos x
x = arccos (-0,881)
x2 = 2,6488 (expresado en radianes) / 151º 45’ 59’’ (expresado en grados)
Comprobamos si esta solución x2 = 2,6488 cumple la igualdad en la ecuación inicial:
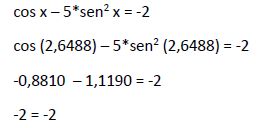
Por lo tanto la solución x2 = 2,6488 es solución de la ecuación inicial.
La función coseno tiene un periodo de 2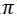 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
1ª solución:
x1 = 0,8216 + 6,2832
x1 = 7,1048 (expresado en radianes) / 407º 04’ 34’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x1 = 0,8216 + (2 * 6,2832)
2ª solución:
x2 = 2,6488 + 6,2832
x2 = 8,9320 (expresado en radianes) / 511º 45’ 59’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x2 = 2,6488 + (2 * 6,2832)
22º ejemplo
sen x * cos x = 0,4
Aplicando la relación trigonométrica:
sen 2x = 2 * sen x * cos x
1/ 2 * sen 2x = sen x * cos x
La ecuación quedaría:
1/ 2 * sen 2x = 0,4
sen 2x = 0,8
2x = arcen (1,6)
2x = 0,9273
x1 = 0,9273 / 2 = 0,4636 (expresado en radianes) / 26º 33’ 54’’ (expresado en grados)
Comprobamos si esta solución x1 = 0,4636 cumple la igualdad en la ecuación inicial:
sen x * cos x = 0,4
sen 0,4636 * cos 0,4636 = 0,4
0,4472 * 0,8944 = 0,4
0,4 = 0,4
Por lo tanto la solución x1 = 0,4636 es solución de la ecuación inicial.
La función seno tiene un periodo de 2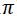 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
2x = 0,9273 + 6,2832
2x = 7,2105
x1 = 3,6052 (expresado en radianes) / 206º 33’ 54’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
2x = 0,9273 + (2 * 6,2832)
23º ejemplo
cos (2x) – cos (6x) = sen (5x) + sen (3x)
Hay que operar con la ecuación con idea de reducir la diversidad de ángulos.
Aplicando la relación trigonométrica:

Aplicando las relaciones trigonométricas:
sen (-x) = - sen(x)
La ecuación quedaría:
sen (4x) * sen (2x) = sen (4x) * cos (x)
Operamos:
sen (4x) * sen (2x) - sen (4x) * cos (x) = 0
sen (4x) * (sen (2x) - cos (x)) = 0
Un producto es igual a 0 cuando cualquiera de sus factores es 0:
a) Igualamos a 0 el primer factor:
sen (4x) = 0
4x = arcsen (0)
4x = 0
x1 = 0 (expresado en radianes) / 0º 0’ 0’’ (expresado en grados)
Comprobamos si esta solución x1 = 0 cumple la igualdad en la ecuación inicial:
cos (2x) – cos (6x) = sen (5x) + sen (3x)
cos (2*0) – cos (6*0) = sen (5*0) + sen (3*0)
cos (0) – cos (0) = sen (0) + sen (0)
1 – 1 = 0 + 0
0 = 0
Por lo tanto la solución x1 = 0 es solución de la ecuación inicial.
La función seno tiene un periodo de 2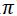 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
1ª solución:
4x = 0 + 6,2832
4x = 6,2832
x1 = 1,5708 (expresado en radianes) / 90º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
4x = 0 + (2 * 6,2832)
b) Igualamos a 0 el segundo factor:
sen (2x) - cos (x) = 0
Aplicando las relaciones trigonométricas:
sen (2x) = 2* sen (x) * cos (x)
La ecuación quedaría:
2* sen (x) * cos (x) - cos (x) = 0
cos (x) * (2* sen (x) – 1) = 0
Un producto es igual a 0 cuando cualquiera de sus factores es 0:
b.1) Igualamos a 0 el primer factor:
cos (x)= 0
x = arccos (0)
x2 = 1,5708 (expresado en radianes) / 90º 00’ 00’’ (expresado en grados)
Comprobamos si esta solución x2 = 1,5708 cumple la igualdad en la ecuación inicial:
cos (2x) – cos (6x) = sen (5x) + sen (3x)
cos (2*1,5708) – cos (6*1,5708) = sen (5*1,5708) + sen (3*1,5708)
-1 + 1 = 1 - 1
0 = 0
Por lo tanto la solución x2 = 1,5708 es solución de la ecuación inicial.
La función coseno tiene un periodo de 2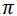 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
x2 = 1,5708 + 6,2832
x1 = 7,8540 (expresado en radianes) / 450º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x2 = 1,5708 + (2 * 6,2832)
b.2) Igualamos a 0 el segundo factor:
2* sen (x) – 1 = 0
sen (x) = 0,5
x = arcsen (0,5)
x3 = 0,5236 (expresado en radianes) / 30º 00’ 00’’ (expresado en grados)
Comprobamos si esta solución x3 = 0,5236 cumple la igualdad en la ecuación inicial:
cos (2x) – cos (6x) = sen (5x) + sen (3x)
cos (2*0,5236) – cos (6*0,5236) = sen (5*0,5236) + sen (3*0,5236)
0,5 + 1 = 0,5 + 1
1,5 = 1,5
Por lo tanto la solución x3 = 0,5236 es solución de la ecuación inicial.
La función seno tiene un periodo de 2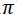 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
x3 = 0,5236 + 6,2832
x3 = 6,8068 (expresado en radianes) / 390º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
x3 = 0,5236 + (2 * 6,2832)
24º ejemplo
sen 2x = 0
2x = arsen (0)
2x = 0
x1 = 0 (expresado en radianes) / 0º 00’ 00’’ (expresado en grados)
La función seno tiene un periodo de 2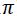 (360º / 6,2832 radianes); luego también serán solución de la ecuación:
(360º / 6,2832 radianes); luego también serán solución de la ecuación:
2x = 0 + 6,2832
x1 = 3,1416 (expresado en radianes) / 180º 00’ 00’’ (expresado en grados)
La solución se irá repitiendo cada 360º.
2x = 0 + (2 * 6,2832)