Ecuación de grado superior a 2 con una incógnita
Una ecuación de grado superior a 2 con una incógnita la podemos escribir en forma de polinomio P(x) = 0.
Por ejemplo, una ecuación de tercer grado con una incógnita tendría la forma canónica:
ax3 + bx2 + cx + d = 0
Y una ecuación de grado “n” con una incógnita:
a1xn + a2xn-1 + a3xn-2 + … + an-2x2 + an-1x + an = 0
En este curso vamos a analizar métodos de resolución de ecuaciones de tercer grado con una incógnita y de ciertos tipos de ecuaciones de cuarto grado con una incógnita.
Ecuación de tercer grado
La ecuación de tercer grado con una incógnita se denomina ecuación cúbica.
Su forma canónica es:
ax3 + bx2 + cx + d = 0
Los coeficientes pueden ser iguales a 0 a excepción de “a” que siempre tiene que ser distinto de 0.
Veamos un ejemplo:
4x3 + x2 - 3x + 2 = 3x2 + 2x – 5
Pasamos todos los términos al miembro de la izquierda:
4x3 + x2 - 3x + 2 - 3x2 - 2x + 5 = 0
Simplificamos:
4x3 - 2x2 - 5x + 7 = 0
La ecuación de tercer grado con una incógnita tiene la siguiente representación gráfica:
Ejemplo: 2x3 - x2 + 3x + 4 = 0
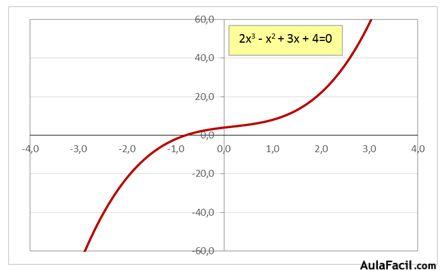
La ecuación de tercer grado tiene siempre tres soluciones si bien puede que no todas ellas sean soluciones reales, no obstante al menos una de las soluciones si tiene que ser real.
La ecuación de tercer grado es una función continua (como podemos ver en los gráficos anteriores) cuyos valores van desde - ∞ a + ∞ por lo que necesariamente esta función tiene que cortar el eje de abscisas (cuando la función toma valor 0), siendo el valor de “x” en ese punto de corte una solución real de la ecuación.
Vimos en el primer gráfico que la función sólo corta una vez el eje de abscisas por lo que esa ecuación tan solo tiene un solución real (las otras dos son complejas).
En cambio en el segundo gráfico la función corta tres veces el eje de abscisas por lo que esa ecuación tiene tres soluciones reales.
En definitiva, en las ecuaciones de tercer grado con una incógnita se pueden presentar tres casos:
a) La ecuación tiene 3 soluciones reales y todas ellas son diferentes.
b) La ecuación tiene 3 soluciones reales pero al menos 2 de ellas son iguales entre sí.
c) La ecuación tiene 1 solución real y 2 soluciones complejas: el número complejo es la suma de una parte real y una parte imaginaria (múltiplo de la unidad imaginaria que se representa con la letra i).


