Definición de ecuación

Una ecuación es una igualdad entre dos expresiones matemáticas:

3x + 6 = 2y

Vemos en el ejemplo anterior que en una ecuación hay valores conocidos, representados por números, y valores desconocidos, representados por letras:

• Los valores conocidos de denominan “datos”
• Los valores desconocidos ya dijimos que se denominan “incógnitas” o “variables”.

En la ecuación hay dos expresiones matemáticas (una situada a la izquierda del signo igual y otra situada a su derecha). Estas expresiones matemáticas se denominan “miembros de la ecuación”.

En cada miembro hay diversos sumandos que se denominan términos.

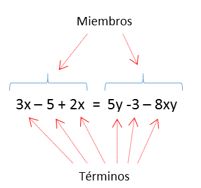
Los términos que llevan incógnitas (en el ejemplo anterior “3x”, “25y”…) se llaman términos dependientes, mientras que aquellos términos que no llevan incógnitas (“5” y “6”) se denominan términos independientes.

Resolver una ecuación es hallar aquellos valores de las incógnitas que hace que la igualdad entre los dos miembros de la ecuación se cumpla. Estos valores que resuelven la ecuación se denominan soluciones o raíces de la ecuación.

3x + 4y = 3z

Si x = 2; y = 3 y z = 6

Tenemos:

(3*2) + (4*3) = (3*6)

6 + 12 = 18

18 = 18

Puede ocurrir, como en el ejemplo anterior, que existan efectivamente valores de las incógnitas que haga que la igualdad se cumpla (la ecuación tiene solución), pero también puede ocurrir que no existan esos valores (la ecuación no tiene solución).

Cuando la ecuación tiene solución, es decir dándole ciertos valores a la incógnita se cumple la igualdad, se denomina ecuación compatible.

Cuando no hay ningún valor que tome la incógnita que cumpla la igualdad, se denomina entonces ecuación incompatible.

 = 4

Esta ecuación no tiene solución (no hay ningún valor de «x» que la cumpla ya que la raíz cuadrada de un número negativo no existe).

Incluso en el caso de que la ecuación tenga solución sólo ciertos valores de las incógnitas van a permitir que la igualdad entre los dos miembros de la ecuación se cumpla, por ello diremos que una ecuación es una igualdad condicional (es una igualdad cuyo cumplimiento está condicionado a que las incógnitas tomen unos valores determinados).

El valor de las incógnitas que cumple la igualdad se denomina “raíz” o “solución” de la ecuación.

Si cualquier valor que tome la incógnita hace que la igualdad se cumpla entonces diremos que la ecuación es una identidad.

(3x + 2y)² = 9x² + 12xy + 4y²

Tomamos por ejemplo los siguientes valores: x = 3; y = 5

Tendríamos:

(3 x 3 + 2 x 5)² = 9 x 3² + 12 x 3 x 5 + 4 x 5²

19)² = 81 + 180 + 100

361 = 361

También se cumpliría para:

x = 1; y = 2

x = 5; y = 3

x = 4; y = 7

…. Y para cualquier par de valores de “x” e “y”.

Por tanto es ecuación cuando la igualdad tan sólo se cumple para determinados valores de las incógnitas.

Ejemplo:

3x = 12 - x

Simplificamos situando las incógnitas en el miembro de la izquierda.

3x + x = 12

4x = 12

x = 3

Esta igualdad es una ecuación ya que tan sólo se cumple cuando la incógnita “x” toma el valor 3.

Las incógnitas de una ecuación pueden llevar exponentes 1, 2, 3…. El grado de una ecuación viene determinado por el término de la ecuación que tenga mayor grado. El grado de cada término se calcula sumando los exponentes de sus incógnitas.

Veamos un ejemplo:

3x + 5 -2x²yz = 3x³y²

Esta ecuación tiene los siguientes términos:

3x (su grado es 1 ya que la incógnita x está elevada a 1)

5 (su grado es 0 ya que no lleva incógnita; es lo mismo que si llevara una incógnita elevada a 0)

2x²yz (su grado es 4 ya que la “x” está elevada a 2, la “y” elevada a 1 y la “z” también a 1)

3x³y² (su grado es 5 ya que la “x” está elevada a 3 y la “y” elevada a 2)

Por lo tanto el grado de esta ecuación es 5.