Revisión de conceptos estadísticos básicos (II)
Desviación Típica.
La varianza viene dada por las mismas unidades que la variable pero al cuadrado, para evitar este problema podemos usar como medida de dispersión la desviación típica que se define como la raíz cuadrada positiva de la varianza:
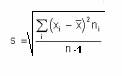
En donde los numeradores representan la suma de las diferencias cuadradas entre los valores medidos y sus medias.
Por último, muchos procedimientos estadísticos hacen uso de la varianza poblacional o de la varianza muestral. La varianza de un conjunto de mediciones es la desviación estándar al cuadrado. De ahí que la varianza poblacional ( ) y de la muestral (s2) se calculen como:
) y de la muestral (s2) se calculen como:
EJEMPLO.
Considérese el siguiente conjunto de edades de personas, en donde se considera que los valores son una muestra de la población, en lugar de la población misma:
23, 38, 42, 25, 60, 55, 50, 42, 32, 35
Para esta muestra, tenemos los siguientes valores:
∑X= 402
N= 10
X= 402/10= 40.2
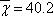
Como se muestra, la media muestral es 40.2 años, la varianza muestral es 148.84 y la desviación estándar muestral es 12.2 años. Si el conjunto de datos originales se hubiera identificado como una población en vez de una muestra, los cálculos habrían sido los mismos, excepto por el denominador en el cálculo de la varianza y la desviación estándar, que sería 10(N) en lugar de 9(n-1). Al término n-1 se le conoce como “grados de libertad”.
El término grados de libertad se utiliza para indicar el número de elementos de datos que son libres de otros en el sentido de que no pueden deducirse de otros, y por tanto,
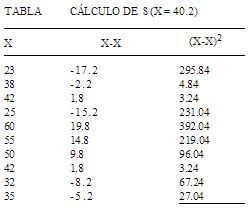
Σ(X-X)2= 1,339.60
Ahora, para obtener la desviación estándar muestral, comenzamos operando el siguiente factor:
(1,339.6)/(10-1)= 148.84
Y a este resultado le calculamos su raíz cuadrada:
s2 = (148.84)½ = 12.2 años.
Todo esto constituye piezas únicas de información. Por ejemplo, suponga que se hacen las siguientes declaraciones:
Pienso en el número 6. Pienso en el número 9. La suma de los dos números en que pensé es 15.
A primera vista, se presentan tres piezas de información. No obstante, si se conocen dos de estas declaraciones, la otra puede deducirse. Se podría decir que en las tres declaraciones sólo hay dos piezas únicas de información o, para usar el término estadístico, que sólo hay dos grados de libertad.
En el ejemplo que se presenta en la tabla anterior, las edades de las diez personas constituyen una muestra con diez grados de libertad. Cualquier edad podría haberse incluido en la muestra, de ahí que cada una de las edades sea libre de variar. Al calcular la media, se usan las diez edades para contabilizar una edad media total de 40.2 años.
En la desviación estándar muestral, el cálculo difiere. Al calcular la desviación estándar muestral, se utiliza una estimación de la media de la población (la media muestral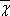 ). Se introduce un sesgo debido a que el valor ∑(Xi-
). Se introduce un sesgo debido a que el valor ∑(Xi-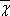 )2 es un valor mínimo para cualquier distribución dada. Si a cada elemento de la distribución se hubiera restado cualquier otro valor distinto de 40.2 y estas diferencias se elevaran al cuadrado y se sumaran, la suma total de cuadrados sería mayor de 1,339.60. Al utilizar en el cálculo la media muestral como una estimación de la media poblacional, por lo regular se obtendrá una desviación estándar menor que la desviación estándar poblacional. Sin embargo, este sesgo se puede corregir dividiendo el valor de Σ(Xi-
)2 es un valor mínimo para cualquier distribución dada. Si a cada elemento de la distribución se hubiera restado cualquier otro valor distinto de 40.2 y estas diferencias se elevaran al cuadrado y se sumaran, la suma total de cuadrados sería mayor de 1,339.60. Al utilizar en el cálculo la media muestral como una estimación de la media poblacional, por lo regular se obtendrá una desviación estándar menor que la desviación estándar poblacional. Sin embargo, este sesgo se puede corregir dividiendo el valor de Σ(Xi-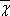 )2 entre el número adecuado de grados de libertad. Ya que la media muestral se usó como una estimación de la media poblacional en el cálculo de la desviación estándar muestral, sólo nueve de las edades son libres de variar. Si se conocen nueve edades, se puede contabilizar la décima, ya que ∑(Xi-
)2 entre el número adecuado de grados de libertad. Ya que la media muestral se usó como una estimación de la media poblacional en el cálculo de la desviación estándar muestral, sólo nueve de las edades son libres de variar. Si se conocen nueve edades, se puede contabilizar la décima, ya que ∑(Xi-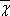 ) debe ser igual a cero. Sólo se requiere de nueve edades para contabilizar la totalidad de la información. En general, siempre que se utilice en un cálculo un estadístico de la muestra como una estimación de un parámetro de la población, se pierde un grado de libertad.
) debe ser igual a cero. Sólo se requiere de nueve edades para contabilizar la totalidad de la información. En general, siempre que se utilice en un cálculo un estadístico de la muestra como una estimación de un parámetro de la población, se pierde un grado de libertad.
Los grados de libertad en un conjunto de datos indican el número de elementos de datos que son independientes de los otros y que se constituyen como piezas únicas de información.
