Revisión de conceptos estadísticos básicos (I)
La mayoría de las técnicas de pronóstico se basa en conceptos estadísticos fundamentales que constituyen el tema de textos sobre estadística en los negocios, así como de cursos de introducción a la estadística. En estas lecciones revisaremos algunos de los conceptos básicos que servirán de fundamento para gran parte del material del resto del curso.
La mayoría de los procesos estadísticos hacen inferencias sobre los elementos de interés denominados población, después de seleccionar y medir un subgrupo de estos elementos llamado muestra. El cuidado en la selección de una muestra representativa y la utilización de un tamaño de muestra lo suficientemente grande, son componentes importantes de un proceso de inferencia estadística con un grado de riesgo aceptablemente bajo.
Junto con la inferencia estadística, la estadística descriptiva constituye la otra gran subdivisión de la estadística. Los procedimientos de estadística descriptiva se emplean para resumir o describir en forma breve conjuntos de datos, de manera que sus componentes esenciales se hagan obvios y se puedan utilizar en el proceso de torna de decisiones.
Estadística Descriptiva
La finalidad de los procedimientos de estadística descriptiva consiste en describir brevemente un gran conjunto de mediciones con unos cuantos valores clave resumidos. La forma más común de lograr esto es promediando los valores. En estadística, el proceso de promediar se lleva a cabo regularmente mediante el cálculo de la media o promedio, lo que comprende sumar todos los valores y dividir entre el número de valores analizados. Debido a que tanto la población como la muestra que se extrae de ella poseen una media, existen dos fórmulas para calcular ésta. La fórmula apropiada depende de que los valores reunidos constituyan todos los valores de interés (la población) o un conjunto parcial de ellos (una muestra).
La estadística descriptiva comprende la descripción de conjuntos de datos por medio de algunos valores clave resumidos.
Por lo regular, los valores de la población o parámetros se identifican utilizando letras griegas. El símbolo elegido para la población es la letra griega u (mu). La fórmula para la media de la población es:
en donde:
åX = la suma de todos los valores de la población
N = el tamaño de la población
El símbolo para la media de la muestra (media muestral) es
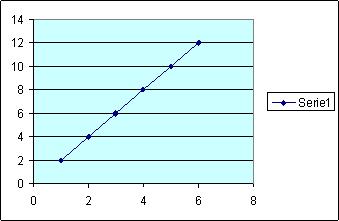(X-barra) y se calcula utilizando la siguiente ecuación:
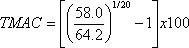
en donde:
Σx= la suma de todos los valores de la muestra
n = el tamaño de la muestra
EJEMPLO.
Calcule la media de la siguiente serie de números:
10, 11, 12, 12, 13.
Los pasos a seguir son:
- Sumar las cantidades < 10 + 11 + 12 + 12 + 13 = 58>
- Dividir la suma por la cantidad de elementos < 58/5>
- El resultado es la media <11.6>
Por lo tanto, la media de los 5 números es 11.6. Note que la media resulta un número que está entre el rango de elementos; en este caso, 11.6 está entre 10, 11, 12 y 13.
Además de medir la tendencia central de un grupo de valores mediante el cálculo de la media, por lo regular es de interés el nivel en el que los valores se encuentran dispersos alrededor de la media, llamado “grado de dispersión”. Para este propósito se puede calcular la desviación estándar de cualquiera de ambos grupos. Se puede pensar en la desviación estándar como en la diferencia típica o estándar entre los valores de un grupo y su media. Las fórmulas siguientes corresponden a la desviación estándar poblacional (a) y muestral (s):
Varianza.
Es el promedio del cuadrado de las distancias entre cada observación y la media aritmética del conjunto de observaciones.
