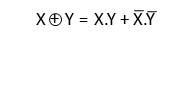Simplificación de Funciones
Combinando los operadores booleanos podemos obtener funciones. De la misma manera que el álgebra tradicional, estas funciones devuelven un sólo resultado, el cual es del mismo tipo de las variables que intervienen, es decir, sólo puede tomar uno de dos valores: FALSO o VERDADERO.
Si una función booleana tiene N variables de entrada, tendrá 2N posibles combinanciones de unos y ceros de entrada, por lo tanto su Tabla de Verdad tendrá exactamente esa cantidad de filas.
Ejemplo:
| A | B | C | (A ^ B) v C |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
Tabla 18-1
La función anterior (A AND B) OR C, tiene tres variables de entrada: A, B y C; por lo tanto, las combinaciones posibles de los valores de entrada es 23 Por este motivo, la Tabla de la Verdad para esta función posee ocho filas. Note que los valores se han representado en su forma binaria: 1 equivale a V y 0 equivale a F.
George Boole ideó una forma de representar estas funciones para facilitar su manipulación. Esta representación se basa en el hecho de que las operaciones booleanas se pueden asimilar en cierta forma con las operaciones del álgebra tradicional. Así, por ejemplo, el AND es el producto booleano y el OR es la suma boooleana. De esta manera la función anteriormente descrita podría escribirse así:
f(A,B,C) = AB+ C
Para representar funciones que sean descritas de forma diferente o tengan operadores desconocidos, se debe hacer así:
- Se escribe la Tabla de la Verdad de la función.
- Se escribe un término por cada fila cuya salida sea 1. Este término estará compuesto por el producto booleano de las variables de entrada de la siguiente manera: las que tengan valor 1 de entrada se escriben en su forma natural, y las que tengan valor 0 de entrada se escriben con una barra encima indicando que están afectadas por el operador NOT.
- Se unen todos los términos con el operador ''+'' booleano.
Utilizando este procedimiento y las Leyes del Algebra Booleana es posible simplificar de una manera significativa algunas de las funciones más complicadas.
Tomemos como ejemplo la Tabla de la Verdad del operador EQUIVALENCIA:
| X | Y | X EQV Y |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Tabla 18-2