Mapas de Karnaugh
Son similares a una Tabla de la Verdad ya que muestran todos los valores posibles de las variables de entrada y la salida resultante para cada valor. También se conocen como Tablas de Karnaugh o diagramas de Veitch. Su invención en 1950 se debe a Maurice Karnaugh, matemático y físico de los Laboratorios Bell.
Un mapa de Karnaugh consiste en la representación en dos dimensiones de la Tabla de la Verdad de la función que se quiere simplificar. Posee un número de celdas igual al número de filas de la Tabla de la Verdad correspondiente, es decir 2N para una tabla de N variables. Las variables se ordenan en función de su peso, de modo que una sola de las variables varía entre celdas adyacentes. Los términos de la Tabla de Verdad se transfieren de forma directa al Mapa de Karnaugh, albergando un 0 o un 1, dependiendo del valor que toma la función en cada fila. Cuando las funciones tienen menos de seis variables se pueden crear fácilmente a mano, pero para funciones de mayor cantidad de variables se puede utilizar un software especializado.
Un mapa de Karnaugh implementa una manera diferente de simplificar los circuitos lógicos. Se pueden transferir los valores lógicos desde una función booleana o desde una tabla de verdad a un mapa de Karnaugh. Se agrupan los ceros y unos en el mapa para visualizar mejor las relaciones lógicas entre las variables, lo que lleva a una función booleana simplificada. Tomemos como ejemplo la construcción del Mapa de Karnaugh para una función OR de dos variables a partir de la Tabla de la Verdad:
| X | Y | X OR Y |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Tabla 19.1
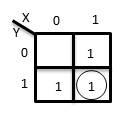
El Mapa de Karnaugh correspondiente sería:
Los valores de una variable se colocan en la parte superior del mapa, definiendo los valores de la columna y los valores correspondientes a la otra variable a un lado, y definen los valores de la variable en cada fila. El mapa de Karnaugh se completa al poner los unos en las celdas que corresponden, copiándolos de la tabla de verdad. Estos se conocen como minitérminos o minterms. No se deben escribir los ceros en el mapa, pues sólo se se van a agrupar los unos. Las celdas vecinas que tienen unos se agrupan de a dos, de a cuatro, o de a ocho. En el caso que nos ocupa, la operación OR, hay un grupo horizontal y otro vertical que se agrupan de a dos. Esto se indica por medio de un círculo que se dibuja alrededor de cada uno. El grupo horizontal corresponde al valor de B = 1, y este valor se mantiene. En esta misma fila, en la celda de la izquierda A = 0 y en la de la derecha A = 1, es decir, la variable A cambia de valor. Quiere esto decir que el valor de la variable A no afecta al resultado final de la expresión booleana para estas celdas. Antes de agruparlas se debe escribir la expresión booleana para estas dos celdas como (NOT (A) AND B) OR (A AND B). Después de agruparlas esta misma expresión se reduce a B
De igual modo, el grupo vertical de dos celdas se puede escribir como (A AND NOT B) OR (A AND B). Puede entonces apreciarse que el valor de B no afecta el valor en las celdas para este grupo. En otras palabras, el grupo vertical se reduce a A. Así el mapa de Karnaugh conduce a la expresión final A OR B. Puede que esto no parezca interesante, pero aplicando este método a un problema más complejo se puede entender cómo con el mapa de Karnaugh simplificar las funciones lógicas y por ende las compuertas que las representan.
Veamos ahora un ejemplo para una función compuesta por tres variables:
Representemos la Tabla de la Verdad para un sistema de elecciones donde participan tres votantes y se gana por mayoría simple.
| X | Y | Z | f(X,Y,Z) |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Tabla 19.2
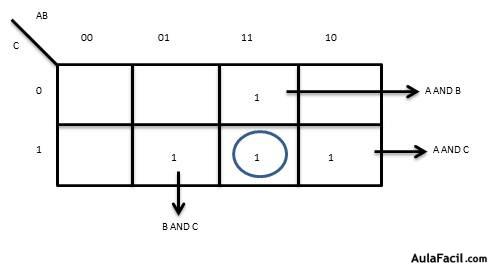
El Mapa de Karnaugh correspondiente se puede apreciar el la figura 19-2.
Los variables correspondientes a las variables A y B no están escritos en forma ascendente 00, 01, 10, 11. Cada una difiere de la anterior en un solo bit, lo que se conoce como código Grey. Esto es con el propósito de que todas las celdas que tengan como resultado uno queden adyacentes. En el mapa de Karnaugh se pueden identificar 3 grupos de dos unos. Todas las celdas que den como resultado cero, se eliminan por lo que la expresión final simplificada sería: (A AND B) OR (A AND C) OR (B AND C). Este método es siempre menos complicado que simplificar la expresión booleana derivada de la tabla de verdad como operaciones OR entre los AND resultantes.
Del mismo modo procederíamos para crear un Mapa de Carnaugh de cuatro y cinco variables pero, como se indicó al principio del capítulo para más de seis variables se hace necesario utilizar un software especializado.