Trabajo Total
Llamamos Trabajo total (Wtot) a la suma de todas las Fuerzas conservativas y NO conservativas.
3.43 A un bloque de 10kg le aplicamos una Fuerza constante de 100N paralela al desplazamiento durante 5 segundos siendo el rozamiento μ = 0,1 ¿cuánto vale el Trabajo?
Respuesta: 1117,7J
Solución
Dibujamos procurando que figuren los elementos expuestos en el texto:
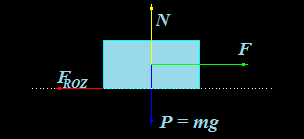
Vemos que la F que aplicamos es paralela al plano horizontal sobre el que el móvil se desliza, lo que nos permite decir que la Normal y el Peso son iguales y sentidos opuestos por lo que se contrarrestan.
Vemos que para calcular el Trabajo desconocemos el camino recorrido y que tenemos la FROZ se opone a F.
Sabemos que: F = m . a que aplicando al problema nos queda:
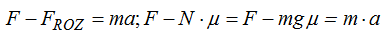
Sustituimos valores que conocemos:
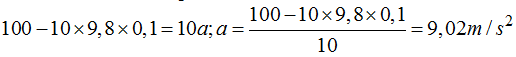
La Fuerza F se ha aplicado de modo constante durante 5s lo que nos permite calcular el espacio recorrido partiendo del reposo:
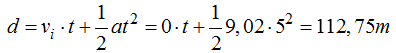
El Trabajo neto nos vendrá dado por el que produce F menos el producido por la FROZ:
WNETO =F.d. cos α – FROZ . d = 10.112,75. 1 – 10 .9,8.0,1 = 1117,7J
3.44 Un coche de 1000kg de peso marcha a una velocidad de 90km/h cuando se encuentra con un obstáculo logrando frenar en 60m.
Calcula el coeficiente de rozamiento entre las gomas de las ruedas y el asfalto del suelo mientras ha durado el frenado.
Respuesta: μ = 0,53
Solución
Nos interesa saber el Trabajo que ha realizado para pasar de 90km/h a 0m/s.
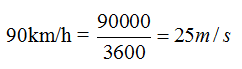
Sabemos que una variación en la Ec supone la existencia de un Trabajo. En este caso, pasa de ir a 25m/s a 0m/s:
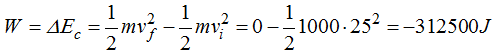
Todos estos Julios han de ser anulados por el Trabajo en la frenada teniendo en cuenta el signo negativo por oponerse al movimiento:
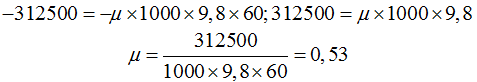
3.45 En la figura siguiente ves en lo alto de un plano inclinado cuyo ángulo mide 30º un objeto de 10 kg de masa que se desliza, sin rozamientos.
Al final del plano inclinado, punto B, el objeto se encuentra con una superficie plana no pulimentada por lo que presenta un valor de μ = 0,3. Gracias a la velocidad de bajada, el bloque venciendo el rozamiento, mientras puede, en la zona llana llega hasta el punto A. ¿Cuál es la distancia entre A y B?
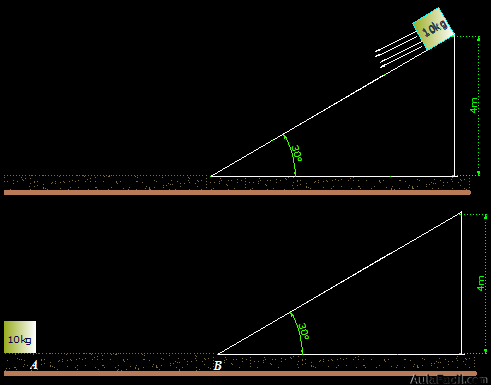
Respuesta: 13,33m
Un modo de resolver muy sencillo es el de calcular la Energía que tiene el bloque en B y a partir de aquí, considerar que toda ella se transforma en WROZ.
Como en la bajada por el plano el bloque, al no haber rozamiento, mantiene su Energía mecánica en todos los puntos (incluido el B) en este punto tendrá el mismo del que tiene en la parte alta del plano inclinado: Ep = mgh = 10.9,8.4 = 392J
El bloque dispone de 392J para trasladarse de B hasta A (distancia que la representamos por x) venciendo un rozamiento de μ = 0,3 lo que nos permite escribir:
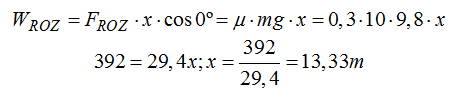
3.46 En la figura siguiente tienes un bloque sobre suelo horizontal:
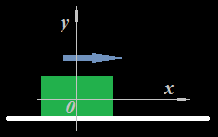
Como resumen de lo que venimos estudiando responde:
a) ¿Cuántas Fuerzas conoces actuando sobre el bloque?
b) ¿Cuántos Trabajos y Energías se producen en el caso de ponerse en marcha en la dirección de la flecha?
Respuesta: Solución
Fuerzas
Fuerza que ejerce la Tierra: P = mg (conservativa)
Fuerza que ejerce el suelo sobre el bloque: N (no conservativa)
(En este caso P = N)
Fuerza que aplicamos: F (no conservativa)
Fuerza de rozamiento: FR (no conservativa)
Trabajos
Trabajo realizado por la Fuerza de la gravedad, WFG
Trabajo realizado por la Fuerza Normal, WFN
Trabajo realizado por la Fuerza aplicada F, WF
Trabajo realizado por la Fuerza de rozamiento, WFR
Trabajo realizado por Fuerzas NO conservativas WFNC
Energías
Variación de la Energía mecánica ΔEm = WFNC
Variación de la Energía cinética ΔEc = WTOTAL
Variación de la Ec, más la variación de la Ep: ΔEc + ΔEp = ∑W
3.47 Al bloque del problema anterior cuya masa es de 10kg le aplicamos una F constante paralela al plano horizontal de 100N. Conocemos la distancia recorrida 20m y μ = 0,15.
Respuestas: 0, 0, 2000J, - 294J y 1706J
Solución
El Trabajo realizado por la F de la gravedad es 0 porque la dirección de ésta con la del desplazamiento forma un ángulo de 90º y si el cos 90º es cero, también lo es el WFG
El Trabajo realizado por la F de la Normal es 0 porque su dirección y la del desplazamiento forma un ángulo de 90º y si el cos 90º es cero, también es lo es el WFN
El Trabajo realizado por la F que aplicamos que es de 100N :
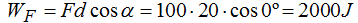
Para conocer el Trabajo realizado por la FR tendremos que hallar primeramente el valor de ella.
FROZ =μ . N
WROZ = FROZ .d = μ . N . d = 0,15. 10.9,8 . 20 = - 294J
El Trabajo Total es:
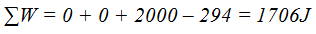
3.48 Un bloque de 5kg se desliza sobre un plano horizontal a una velocidad de 10m/s con rozamiento μ = 0,1.
Después de recorrer 6m choca contra un muelle de 2m de longitud por lo que éste se contrae una longitud Δx.
Del resorte conocemos su constante k = 200N/m
¿Cuánto vale Δx?
Respuesta: 1,81m
Solución
En primer lugar dibujamos la figura correspondiente a la fase (1) antes del choque y en el momento de contracción máxima del muelle, fase (2):
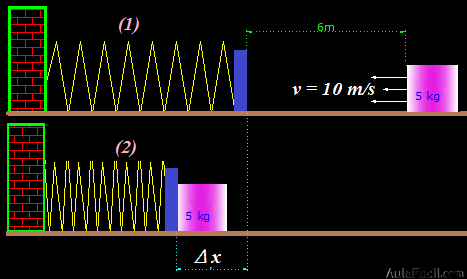
En el escenario que presenta la figura podemos decir que las Fuerzas que llegan a actuar sobre el bloque son:
Fuerza de gravedad- conservativa (mg =5 .9,8 = 49N)
Fuerza Normal-NO conservativa (Normal = 49N)
Fuerza de Rozamiento-NO conservativa (μ.Normal)
Fuerza elástica- conservativa (-k . Δx)
*Calculamos el valor de la Energía mecánica en la posición (1):
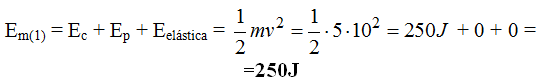
La Ep vale 0J porque no hay altura, el bloque está sobre el suelo.
La Eelástica vale 0J porque se encuentra en reposo.
*Calculamos el valor de la Energía mecánica en la posición (2):
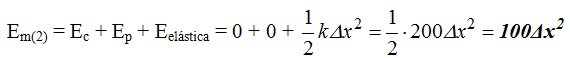
La Ec vale 0J porque se la ha cedido al muelle.
La Ep vale 0J porque el bloque se halla sobre el suelo.
La Eelástica vale 100Δx2 (Energía que ha transmitido la Ec al resorte).
*No hemos de olvidarnos del Trabajo producido por la Fuerza de rozamiento que con los datos que tenemos equivale a:
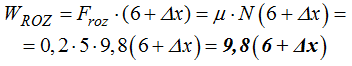
Observa que el espacio recorrido por el bloque hasta el instante de quedar completamente detenido, es 6 + Δx.
Sabemos que cualquier variación en la Em significa la existencia de un Trabajo hecho por fuerzas NO conservativas, ΔEm = WFNC lo que nos permite escribir:
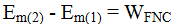
Sustituyendo por los valores que conocemos tenemos:
100Δx2 - 250 = 9,8(6 + Δx) que ordenando nos queda:
100Δx2 - 9,8(6 + Δx) - 250 = 0
todo se ha reducido a una ecuación de 2º grado.
Quitamos el paréntesis y reducimos términos semejantes:
100Δx2 - 9,8 Δx – 58,8 - 250 = 0; 100Δx2 - 9,8 Δx - 308,8 = 0
Resolvemos la ecuación tomando el valor positivo de Δx:
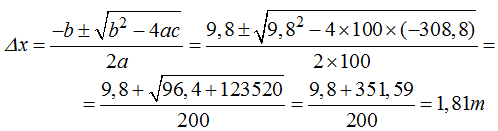
3.49 La siguiente figura representa un muelle en el instante de haberse comprimido (1m) por causa de la Ec que llevaba el bloque. En el instante siguiente en el que el muelle (k = 400 N/m) recobre su longitud normal, el bloque saldrá despedido.
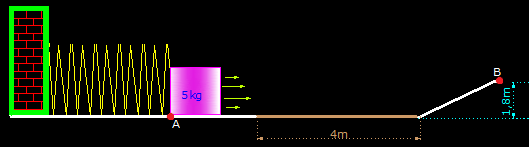
Seguirá el camino horizontal para después ascender por un pequeño plano inclinado de 1,8m de altura.
En este recorrido tienes, el camino señalado con línea blanca sin rozamientos, con color marrón con rozamiento cuyo valor es de
¿Qué velocidad lleva el bloque a su paso por el punto B?
Respuesta: 6,07m/s
Solución
Observo que hay una Fuerza No conservativa (rozamiento en 4m) lo que me dice que la Em en el punto A (EmA) es distinta a la Em en el punto B (EmB).
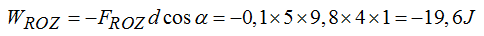
Puedo decir que la EmB - EmA = -19,6J (I)
La Energía mecánica en B vale:
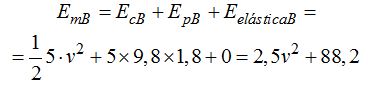
La Energía mecánica en A vale:
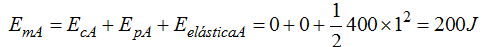
Sustituimos valores en (I):
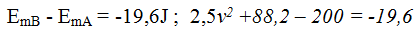
Despejamos el valor de v:
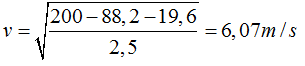
3.50 En la figura que tienes a continuación ves en (1)
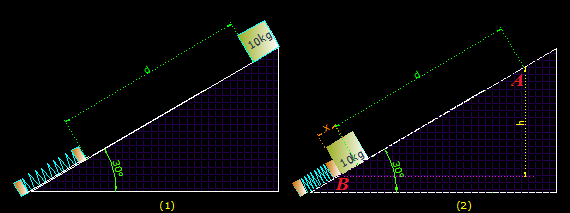
un bloque de 10kg a punto de deslizarse por un plano inclinado de 30º con rozamiento μ = 0,1 y una longitud de 6m. En la parte baja del mismo hay un resorte de k = 200 N/m cuya longitud, en su estado natural, es de 2m.
En (2) el bloque en su deslizamiento sobre el plano inclinado comprime al muelle una distancia x.
¿Cuánto mide la contracción del muelle?
Respuesta: 1,77m
Solución
Como existe una Fuerza NO conservativa, la del rozamiento, significa que la diferencia de las Em en los puntos B y A corresponde al Trabajo realizado por la Fuerza NO conservativa que nos permite escribir:
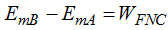
Dada la existencia de un resorte tenemos en cuenta la Eelástica.
La igualdad anterior la escribimos:
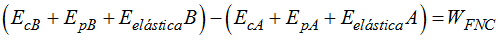
Analicemos los valores de cada tipo de Energía en B y en A:
¿Cuánto vale la Energía cinética en B en el instante que el muelle permanece contraído?
En este momento no hay velocidad por lo que tampoco habrá Ec.
¿Cuánto vale la Energía potencial en B en el momento que el muelle está contraído?
Si nos atenemos a la fórmula de la Ep = mgh vemos que la altura corresponde al origen, es decir, y = 0, lo que es lo mismo, no hay valor de la altura. Significa que tampoco existe Ep.
¿Cuánto vale la EelásticaB? En el momento de contracción del muelle ha acumulado toda su Energía elástica por lo que:
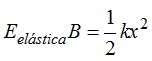
¿Cuánto vale la Energía cinética en A?
Como el bloque comienza a deslizarse a partir del reposo, la velocidad inicial es 0, luego su Ec también valdrá 0.
¿Cuánto vale la Energía potencial en A?
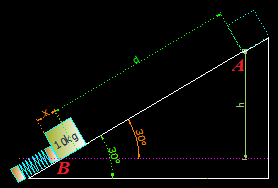
Según vemos en la figura,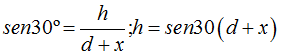 
Significa que la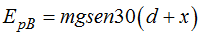 
¿Cuánto vale la EelásticaB? Si no hay resorte tampoco habrá Eelástica.
La igualdad que escribimos anteriormente:
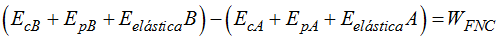
Se nos ha convertido en: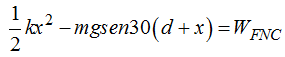 
Calculamos WFNC y para ello dibujamos la figura que nos permite realizar nuestro trabajo de un modo más sencillo:
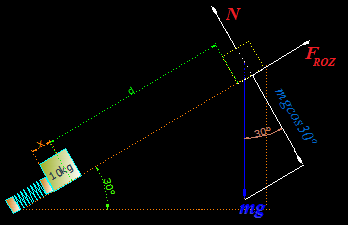
Descomponemos en dos componentes la Fuerza de la gravedad mg y vemos que su componente perpendicular al plano inclinado corresponde a:
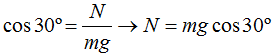
Escribimos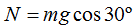 
porque la componente perpendicular al plano (inclinado en este caso) del Peso ha de ser igual a la Normal porque la suma de todas las fuerzas referidas al eje y han de sumar 0.
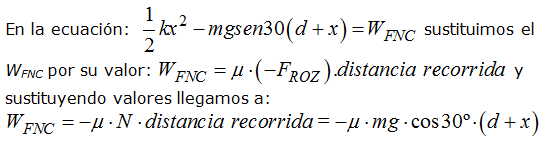
Sustituimos este último valor en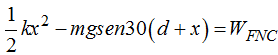 
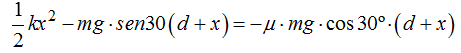
Continuamos haciendo sustituciones de valores que conocemos y vamos efectuando operaciones:
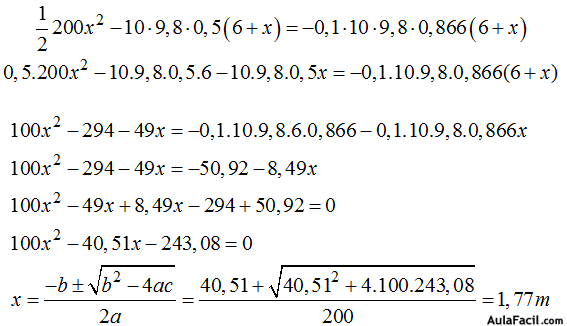
No tenemos en cuenta la segunda respuesta de la ecuación por ser negativa.
