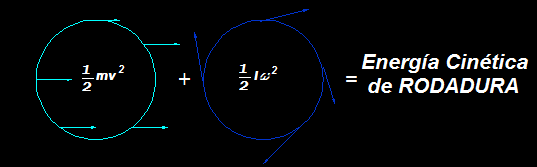
Correspondencia entre la energía cinética de traslación y la energía cinética de rotación
La Energía cinética de Rotación es una forma de la Energía cinética de Traslación.
Su correspondencia la indicamos en el esquema siguiente:
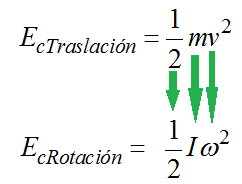
3.57 En la figura siguiente tienes un cilindro de radio r, masa m, a la izquierda se desliza por un plano inclinado de αº apoyado sobre su generatriz.
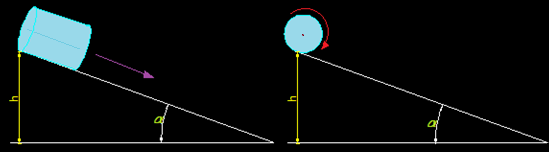
Este plano inclinado ofrece un escaso rozamiento que le permite girar alrededor de su eje.
La altura del plano inclinado es la misma en ambos casos.
¿En qué caso, razonando tu respuesta, la velocidad de llegada al plano horizontal es mayor?
Respuesta: por deslizamiento.
Solución
En el caso de deslizamiento sin rozamiento su Ec vale, suponiendo v su velocidad a la llegada del plano horizontal:
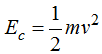y equivale a la 
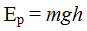lo que significa: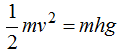 
donde simplificando por m y despejando el valor de v hallamos:
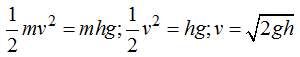
Veamos ahora la velocidad v’ de llegada al plano horizontal en el caso de que el descenso lo haga rodando por el casi inapreciable rozamiento.
En este caso la Ep es la misma que en el caso anterior pudiendo establecer la siguiente igualdad:
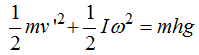
En Dinámica estudiamos que el momento de Inercia de un cilindro macizo es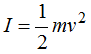 
por lo que sustituimos en la igualdad anterior:
Estudiamos en Cinemática de la Rotación que la velocidad lineal v equivale a la velocidad angular ω . r (radio), es decir: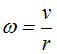 
que sustituyo en la igualdad anterior y simplificamos:
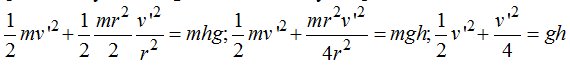
Haciendo operaciones:
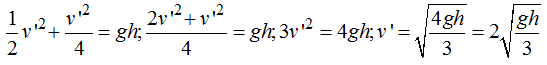
Vemos que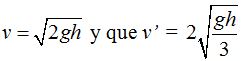 
Para saber cuál de las dos velocidades es la mayor dividimos el valor de una por el de la otra, si el cociente es mayor que 1 diremos que la primera es mayor, si es igual a 1 será porque ambas son iguales y si el cociente es menor que 1 significará que el valor de la 2ª velocidad es mayor:
Dividimos ambas velocidades y vamos haciendo operaciones paso a paso:
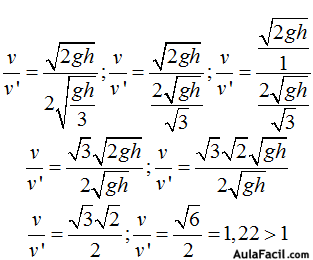
Como el cociente es mayor que la unidad significa que v > v’
También podríamos haber comparado ambas velocidades del siguiente modo:
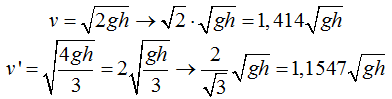
Vemos, a simple vista, que la velocidad por deslizamiento ha sido mayor.
