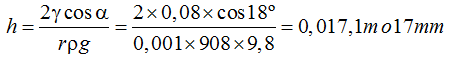¿Cómo se puede calcular la altura que un líquido que moja puede alcanzar en un tubo capilar?
Existen varios procedimientos, pero uno muy sencillo sería el siguiente:
Recordarás que hace muy pocas páginas estudiamos que cuando
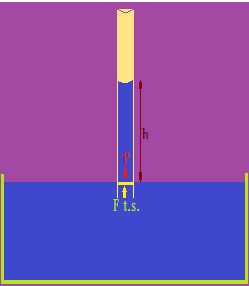
el peso de la columna de agua se iguala con la Fuerza de tensión superficial, en ese instante, ha alcanzado la máxima altura.
Calculamos el Peso de la columna de líquido contenido en el tubo capilar.
Sabemos que 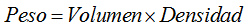
Tenemos en cuenta que el tubo capilar es un cilindro.
r el radio del tubo capilar.
γ a la Fuerza de tensión superficial.
α el ángulo de contacto.
ρ a la densidad del líquido.
g la aceleración de la gravedad de la Tierra.
Sabiendo que el Peso o Fuerza es igual a:
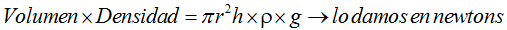
El volumen del cilindro es igual al área de la base por la altura.
Hemos llegado a que el Peso-fuerza del líquido contenido dentro del tubo capilar es: 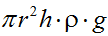
Este Peso debe ser igual a la Fuerza de tensión superficial que tiene en la base.
La Fuerza de la tensión superficial depende del ángulo de contacto:
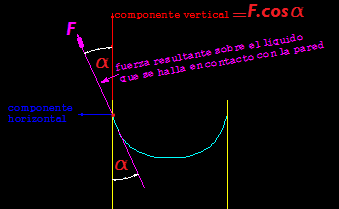
La fuerza F resultante tiene las componentes que se indican y de ellas nos interesa la vertical: F. cos α
Esta Fuerza se ejerce alrededor de la longitud circular de la superficie del líquido en contacto con la pared interna del tubo capilar.
A medida que el ángulo se hace menor el factor cos α se hace mayor. Ya sabes que el cos 90º = 0 y cos 0º =1:
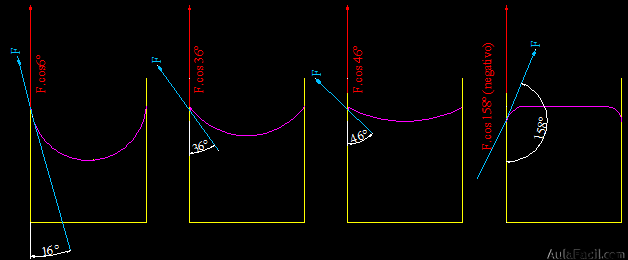
A medida que más moja menor es el ángulo de contacto.
En el caso del mercurio el ángulo supera 90º, luego al menisco lo consideramos “negativo”.
En el caso de que una gota de agua y otra de mercurio se nos cayeran sobre una lámina de vidrio las veríamos más o menos con estos ángulos de contacto:
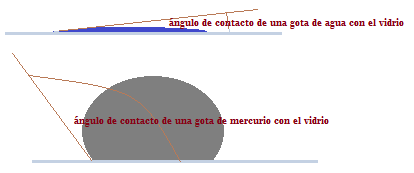
Continuamos con nuestros cálculos y haciendo uso de la unidad de la tensión superficial gamma (γ) estudiada anteriormente.
Sabemos que la longitud de la circunferencia es y si γ es la fuerza de tensión superficial por unidad de longitud llegamos a:
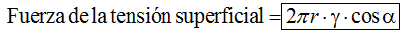
Los valores enmarcados son iguales, es decir:
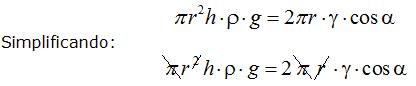
Despejamos el valor de h:
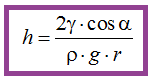
Resumen de las unidades utilizadas:
Símbolo | Variable referida a: | Expresamos en: |
γ | Tensión superficial | N/m |
ρ | Densidad del líquido | Kg/m3 |
α | Ángulo de contacto | Grados |
r | Radio del tubo capilar | M |
g | Aceleración gravedad | m/s2 |
Nota: Las unidades están expresadas en el Sistema Internacional (SI).
4.38 Supongamos que tenemos un tubo de 0,001m de radio, un líquido cuya tensión superficial equivale a 0,08 N/m, su densidad es de 908 kg/m3 y el ángulo de contacto de 18º en un lugar donde la aceleración de la gravedad de la Tierra es de 9,8 m/s2.
Con estos datos, calcula la altura a la que asciende este líquido dentro del tubo indicado.
Respuesta: 17mm
Solución
No tenemos más que aplicar la fórmula: