Representación de los espejos esféricos en un eje de coordenadas
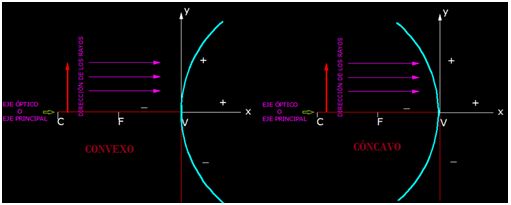
Ten en cuenta que en el eje de abscisas o eje de x cuanto se halla a la derecha del centro de la figura V es positivo y negativo hacia la izquierda.
Respecto al eje de ordenadas o eje de y es positivo cuanto se halla sobre el eje principal y negativo debajo del mismo.
Los problemas tratan generalmente del cálculo de las distancias de las posiciones de objetos o imágenes y de sus tamaños.
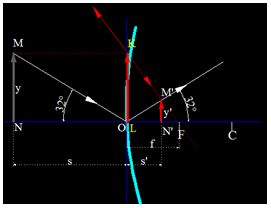
Observa la siguiente figura:
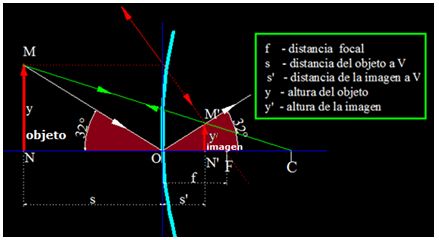
El objeto MN se refleja en un espejo convexo y obtenemos la imagen virtual M’N’.
La distancia focal es f (desde el foco a O).
La distancia del objeto a O es s.
La distancia de la imagen a O es s´.
Observa que los triángulos MNO y M’N’O son semejantes:
¿Por qué decimos que son semejantes?
Porque si te fijas bien los ángulos de ambos triángulos son iguales.
Si los triángulos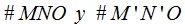 
son semejantes, sus lados son proporcionales.
Significa que podemos formar las proporciones siguientes:
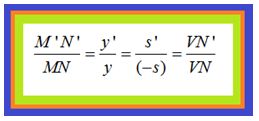
Ten en cuenta que el valor de s es negativo. Recuerda que los valores de x a la izquierda del centro de coordenadas son negativos.
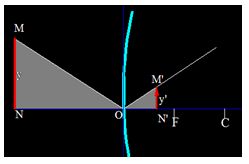
Trasladamos el objeto a la posición que ves en la figura siguiente:
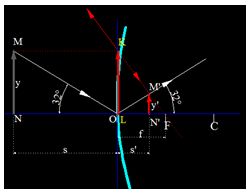
Los triángulos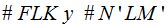 
de la siguiente figura son triángulos rectángulos, luego, son semejantes y sus lados proporcionales:
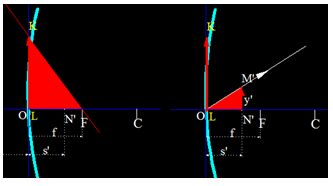
Vamos a establecer las siguientes proporciones teniendo en cuenta la figura anterior, procurando prestar mucha atención:
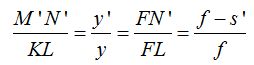
La diferencia entre la distancia focal f y la distancia entre la imagen y el vértice del espejo s’ equivale a la distancia FN’.
De estas proporciones tomamos: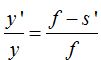 
(I) Anteriormente obtuvimos: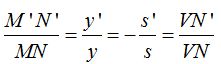
El signo menos lo hemos colocado delante de la fracción dado que s tiene valor negativo.
De estas proporciones extraemos: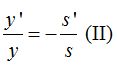 
Hemos llegado a: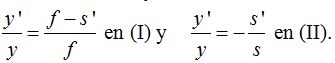 
Esto nos permite escribir: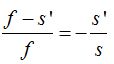 
Hacemos operaciones poniendo cuidado en las operaciones que vamos a hacer.
En la proporción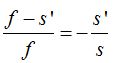 
lo primero que hacemos en el primer miembro de la igualdad es dividir a cada término del numerador por el denominador:
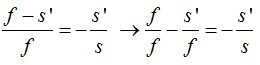
Simplificando la primera fracción me queda: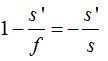 
Divido a cada término de la igualdad por s’: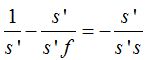 
Simplificando obtengo: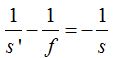 
Despejo al inverso de la distancia focal teniendo cuidado con los signos y obtengo la ecuación de los espejos:
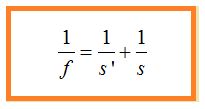
Esta fórmula la podemos modificar haciendo intervenir al radio de un espejo.
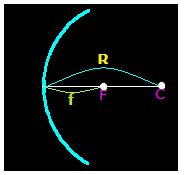
Si el radio del espejo esférico es R sabemos que el foco F se halla a la mitad de la distancia entre el centro del espejo y el centro de curvatura C.
Esto significa que R =2f o bien, r = 2f y despejando el valor de f llegamos a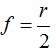 
y sustituyendo este valor en la fórmula anterior y haciendo operaciones paso a paso llegamos a:
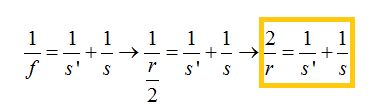
Esta ecuación nos sirve para calcular las distancias de las posiciones de imágenes y objetos.
