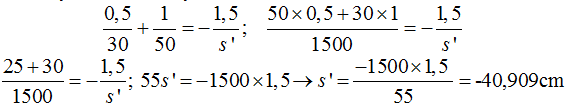Dioptrio
Hemos estudiado espejos, refracción y reflexión de los rayos de luz y poca cosa más, pero nos encontramos con situaciones en las que a un mismo tiempo, la luz se desplaza por dos medios transparentes diferentes, de índices de refracción distintos:

En las fotografías (la de la izquierda está tomada en el Aquarium de San Sebastián) ves al mismo tiempo dos medios diferentes por donde pasa la luz: aire - agua y aire - vidrio.
El comportamiento del rayo de luz a través de dos medios transparentes diferentes es lo que a continuación vamos a tratar de comprender entendiendo que en todos los casos el sentido de la dirección de los rayos de luz es de izquierda a derecha.
Antes de comenzar a estudiar el dioptrio conviene que tengas clara la idea del significado de la palabra sistema.
Utilizamos la palabra sistema cuando nos referirnos, por ejemplo, al sistema métrico decimal, al sistema nervioso de nuestro cuerpo, al sistema operativo de nuestro ordenador, al sistema digital en electrónica, etc.
Si te fijas un poco verás que en cada sistema los elementos que lo componen se relacionan entre sí.
El metro tiene que ver con el kilómetro, hay una relación entre ellos.
Las malas posturas tienen que ver con ciertos dolores de espalda o algunos problemas con la columna vertebral.
Los archivos del sistema operativo nos permiten trabajar con un ordenador, realizar diversas tareas, etc.
Con la palabra dioptrio que significa que tiene que ver con la refracción de la luz es un sistema óptico en el que hay una superficie (puede ser plana o curva), que separa dos medios transparentes que tienen distinto índice de refracción:
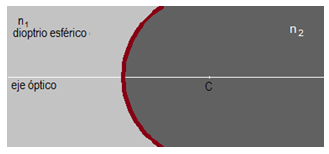
Vemos en la figura dos medios de índices de refracción diferentes n1 y n2 separados por una superficie esférica cuyo centro se halla en C y es el dioptrio esférico, en este caso.
En la figura que tienes a continuación fijamos en A un objeto
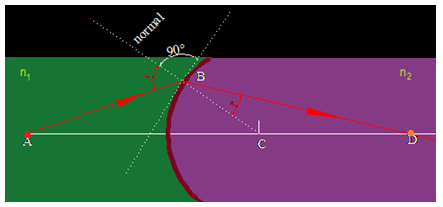
Luminoso que emite, entre los numerosos rayos, uno que incide en B formando con la normal un ángulo i.
Este rayo llega a la superficie de separación en B.
Al penetrar en un medio de mayor índice de refracción se refracta llegando a cortar al eje óptico en D y formando en este punto la imagen de A.
Observa en la figura que tienes a continuación los ángulos α (alfa), β (beta) y γ(gamma) son ángulos muy pequeños.
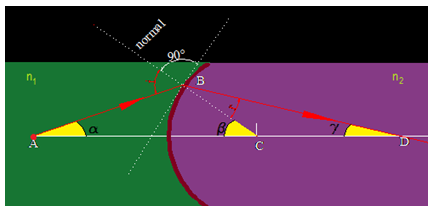
A sus valores, al de sus senos y al de sus tangentes les consideramos iguales.
Recordamos algo de lo estudiado en Geometría relativo a los triángulos:
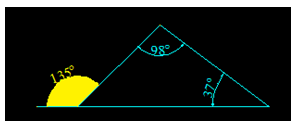
Un ángulo exterior es igual a la suma de los dos interiores no adyacentes a él.
La suma de los ángulos interiores 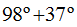 equivale al valor del exterior no adyacente o no contiguo a ninguno de ellos, 135º.
equivale al valor del exterior no adyacente o no contiguo a ninguno de ellos, 135º.
En la siguiente figura puedes ver que el ángulo de incidencia i es un ángulo exterior del triángulo 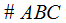 :
:
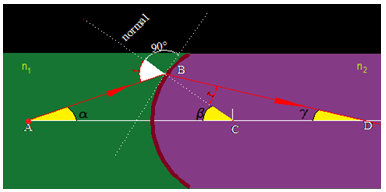
y podemos escribir la igualdad: 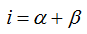
Lo mismo sucede con el ángulo 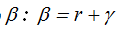 que lo compruebas en la figura:
que lo compruebas en la figura:
Para facilitar cálculos trazamos la altura común a los dos triángulos a los que nos hemos referido:
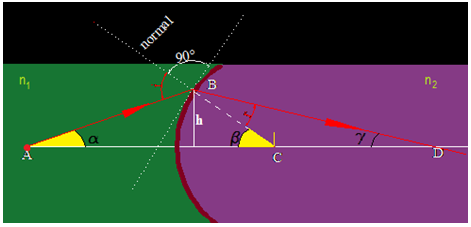
Volvemos a nuestra fórmula tantas veces utilizada:
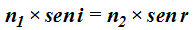
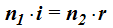 (I)
(I)
Porque se tratan de ángulos muy pequeños en radianes.
Hemos estudiado que 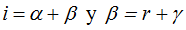
Despejamos el valor de 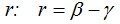
Sustituimos estos valores en (I):
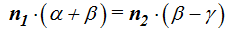 (II)
(II)
Establecemos las distancias del objeto luminoso A hasta la superficie esférica: s y desde la imagen D hasta la superficie esférica: s’ siendo O el vértice del dioptrio :
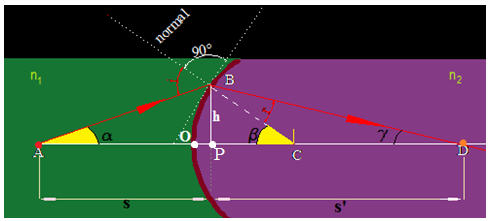
El radio de la superficie esférica CB que la representamos con R equivale también a OC porque al tratarse de rayos muy próximos al eje óptico la distancia OP es casi nula y BP es muy pequeña. Haciendo uso de lo estudiado en Trigonometría:
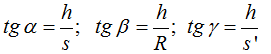
Sabemos que por tratarse de ángulos pequeños aceptamos las igualdades siguientes:
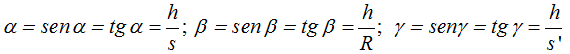
Estos valores sustituimos en (II): 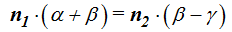
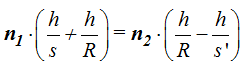
Podemos simplificar todos los términos por h y nos queda:
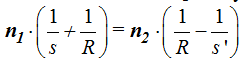
Hacemos operaciones eliminando los paréntesis:
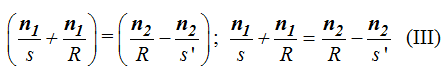
Pero cuidado, la distancia s se halla a la izquierda del vértice O que lo consideramos como eje de abscisas lo que significa que tiene signo negativo por lo que la fórmula en (III) se nos convierte en:
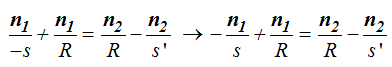
Dejamos a un lado de la igualdad los términos que tienen el mismo denominador y al otro los que lo tienen diferente:
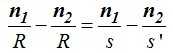
Como tienen el mismo denominador podemos restar los numeradores dejando el mismo denominador:
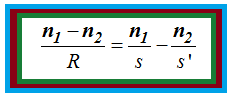
Esta es la fórmula fundamental del dioptrio esférico.
5.27 Al estudiar lo que antecede, a veces, surge la idea de resolver algún problema que tenga que ver con una pecera.
Para ser fieles a este hecho observa la fotografía siguiente:

Es en la pecera donde vemos con claridad la superficie esférica que divide dos medios transparentes de distinto índice de refracción.
Supongamos que la pecera tiene 40 cm de Radio a la altura donde se halla el pez rojo.
Tomamos como referencia el pez rojo por tener un detalle con el gato. A éste el rojo le apetece más, le recuerda al besugo.
El pez está situado a 20 cm de la pared interna de la pecera.
¿A qué distancia le ve (a la imagen) la analítica niña?
Del gato no te pregunto nada, su mirada no es de admiración por la belleza del pez.
Respuesta: -17,14cm
Hacemos un sencillo esquema con los datos del problema:
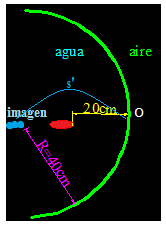
Los ponemos con signos negativos por estar representados sobre el eje de abscisas y a la izquierda del vértice O de la superficie esférica.
Tenemos que calcular la distancia s’.
Colocamos los datos que conocemos:
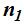 índice de refracción de la luz en el agua 1,33 aunque desde
índice de refracción de la luz en el agua 1,33 aunque desde
este momento y para ser más exactos lo tomamos como 4/3.
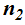 índice de refracción de la luz en el aire 1.
índice de refracción de la luz en el aire 1.
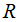 radio 40cm.
radio 40cm.
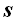 distancia conocida a la que se encuentra el objeto de la
distancia conocida a la que se encuentra el objeto de la
superficie esférica 20cm.
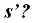
Aplicamos la fórmula: 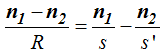
Sustituimos valores y hacemos operaciones paso a paso:
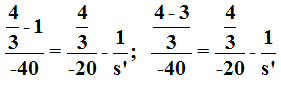
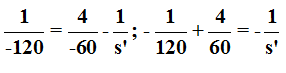
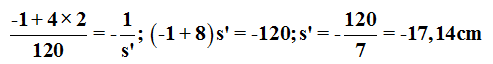
A la guapa y estudiosa niña le parece que su pez rojo se halla a 17,14cm próximo a la pared interior transparente de la pecera.
5.28 Delante de un dioptrio esférico cóncavo de 30cm de radio y a 50cm de él se halla situado un objeto. Si los índices de refracción son n1 = 1 y n2 = 1,5 calcula la posición de la imagen.
Respuesta: -40,9cm
Hacemos el dibujo que siempre es una ayuda:
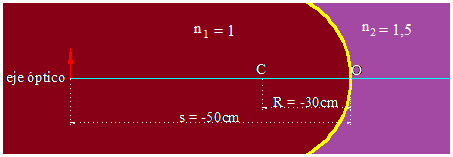
Tomamos la fórmula:
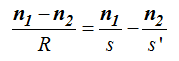
Sustituyendo valores y haciendo operaciones: