Desviación que sufre un rayo al atravesar un prisma óptico
Vamos a estudiar la desviación que sufre un rayo de luz desde que incide en una cara lateral del prisma hasta que sale o emerge del mismo.
Tratamos de estudiarlo paso a paso. No ofrece dificultades.
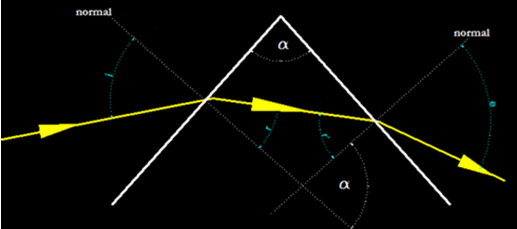
El ángulo α es el ángulo del prisma óptico.
Hemos señalado dos ángulos α y verás que dichos ángulos son iguales por estar comprendidos en lados perpendiculares.
El rayo amarillo incide en una cara del prisma que al ser de un material transparente se refracta dado que tiene un índice de refracción superior al aire y crea, en un primer momento, un ángulo de incidencia i y el de refracción r.
Dentro del prisma, el rayo refractado continúa su trayectoria hasta llegar a la otra cara.
En el momento de llegar el rayo refractado incide en esta segunda cara creando un ángulo que por venir refractado lo representamos con r’ y emerge al medio aire separándose de la normal con un ángulo e por encontrarse con un medio menos refringente.
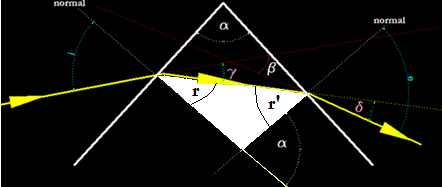
Si prolongamos las direcciones del rayo a la entrada y a la salida con líneas discontinuas rojas, se forma un ángulo β, se trata del ángulo que se ha formado por las desviaciones que ha tenido el rayo.
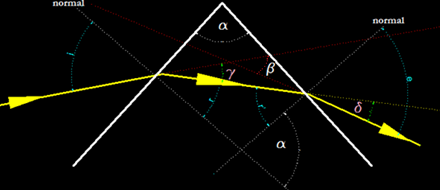
En esta nueva figura que tienes seguidamente hemos añadido dos nuevos ángulos γ y δ: nos indican las desviaciones que ha tenido el rayo.
Ves que al ángulo δ la hemos colocado dentro del triángulo gris.
Ambos son iguales por ser opuestos por el vértice.
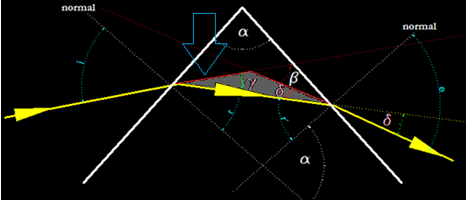
Observa el triángulo gris:
Tiene dos ángulos interiores que son γ y δ y uno exterior β.
Sabemos que la suma de dos ángulos interiores equivale al ángulo exterior no adyacente, es decir:
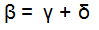
Si te fijas en la figura verás que el ángulo de incidencia i equivale a la suma de los ángulos γ + r por ser opuestos por el vértice.
Despejamos γ: γ = i - r
El ángulo e de emergencia vale lo mismo que la suma de δ + r’:
En la igualdad obtenida anteriormente: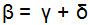 
sustituimos que acabamos de obtener: β = i – r + e – r’
Esta igualdad podemos escribirla también: β = i + e – (r +r’) (I)
Ahora debes fijarte en el triángulo blanco:
Ves que la suma de los ángulos interiores r + r’ vale lo mismo que el exterior α.
β = i + e – (r +r’) → β = i + e – α
Esta fórmula puede servirte para calcular la desviación que sufre un rayo a su paso por un prisma óptico:
5.43 Un rayo de luz procedente del aire incide en una de las caras de un prisma de 70º con un ángulo de 59º.
Calcula el ángulo de desviación sufrido por el rayo a su paso por el prisma óptico.
Respuesta: 66,52º
El objetivo es conocer los ángulos i y e para aplicar la fórmula que acabamos de deducir.
Nos ayudamos de un dibujo:
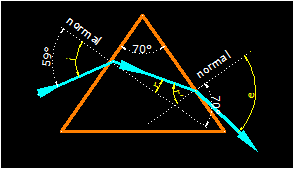
Cuando estudiamos la refracción dedujimos la fórmula:
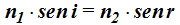
Es la que nos va a servir para calcular el valor del ángulo r y sustituyendo valores que conocemos conseguimos:
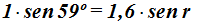
Despejamos sen r: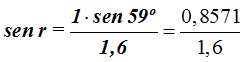 
Hallamos a cuántos grados de arco corresponde seno anterior:
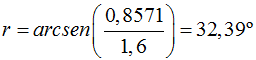
Conocido el valor de r nos es fácil saber el de r’.
Fíjate en el triángulo relleno de color morado:
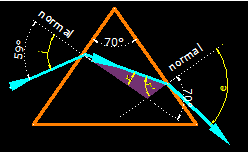
Ves que la suma de los dos ángulos interiores r + r’ equivale al exterior no adyacente: r + r’ = 70º.
r’ = 70 - 32,39 = 37,61º
Ya hemos calculado la primera desviación.
Ahora tenemos que calcular la siguiente refracción (salida del rayo) que nos permitirá conocer el valor del rayo emergente e y para ello volvemos a tomar la fórmula anterior teniendo en cuenta que el rayo “camina” dentro del prisma óptico donde el índice de refracción es 1,6 y al salir del prisma vuelve al medio aire donde el índice de refracción vale 1:
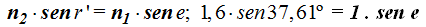
Despejamos sen e y haciendo operaciones obtenemos:
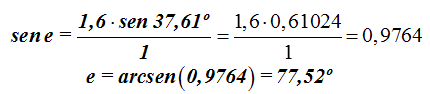
Tomamos la fórmula de la desviación: β = i + e – α sustituyendo valores obtenemos: β = 59º + 77,52º – 70º = 66,52º
Ángulo incidente 20º
Índice de refracción del material del prisma 1,4
Calcula la desviación que ha sufrido el rayo.
Respuesta: 17,63º
