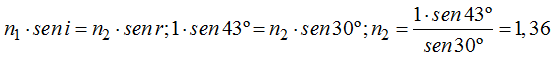Ángulo de desviación mínima
La desviación del rayo a su paso por el prisma óptico será mínima cuando su trayectoria sea paralela a la base como puedes comprobar en la figura siguiente:
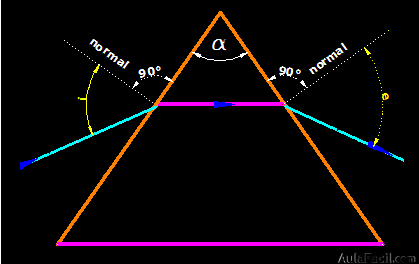
Ves que la trayectoria del rayo de luz dentro del prisma es paralela a la base.
Esta circunstancia implica que los ángulos de incidencia (i) y de emergencia (e) son iguales.
Si son iguales estos dos ángulos significa que las refracciones del rayo en el interior del prisma son iguales, es decir: r = r’
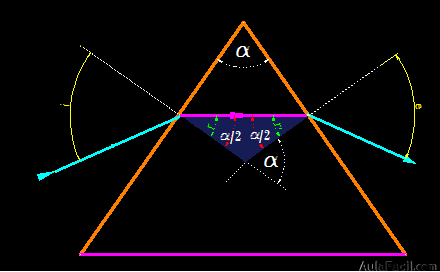
Fíjate en el triángulo azul, la suma de los ángulos interiores:
r + r’ es igual al exterior no adyacente. Estos dos ángulos son iguales, luego, r + r = 2r lo que significa que 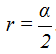 .
.
Tenemos que calcular un ángulo de incidencia (i) para que el rayo en el interior del prisma óptico permanezca en la misma trayectoria.
El problema es el de calcular el ángulo de incidencia para que se produzca el que r y r’ sean iguales.
Nos servimos de:
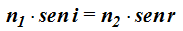
Sustituimos valores:
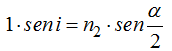
Nos interesa conocer el valor de i:
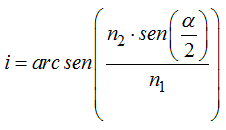
5.45 En una de las caras laterales de un prisma óptico de 70º incide un rayo de luz.
¿Cuál es su ángulo de desviación mínima si el índice de refracción de este prisma es 1,6?
Respuesta: 66,59º
Aplicamos la fórmula que acabamos de obtener, sustituimos valores y hacemos uso de la Trigonometría:
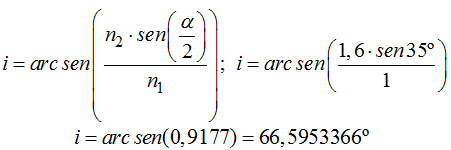
Escribimos los decimales para que veas en la comprobación que efectivamente hemos hecho bien los cálculos:
Comprobación:
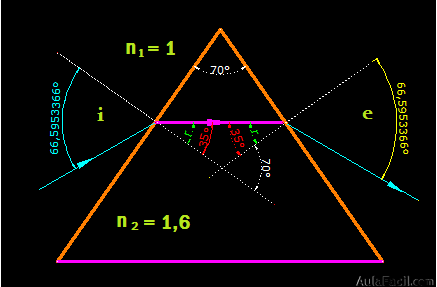
Para que el resultado esté bien realizado ha de suceder que:
Comenzando por la fórmula: 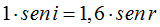
Hacemos sustituciones: 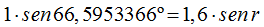
Despejamos sen r y hacemos operaciones:
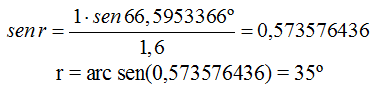
Comprobamos que efectivamente con un ángulo incidente de 66,5953366º se produce un ángulo refracción de 35º, en las condiciones del problema, que se mantiene en su trayectoria interna del prisma.
5.46 Calcula el ángulo de desviación mínima sabiendo que el prisma tiene un ángulo de 60º y un índice de refracción de 1,3.
Tampoco se muestra su solución por ser semejante al anterior.
Respuesta: 40,54º
5.47 Un rayo incide sobre una cara lateral de un prisma óptico de 60º formando con la normal un ángulo de 43º.
Sabemos que la trayectoria del rayo en el interior del prisma es paralela a la base horizontal.
¿Cuánto vale el índice de refracción de este prisma óptico?
Respuesta: n2 = 1,36
Siempre que puedas es mejor que hagas un dibujo aunque sea muy sencillo:
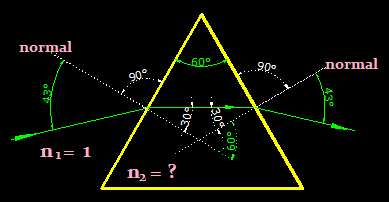
Por lo que nos dice el problema vemos que se trata de un prisma cuya sección es un triángulo equilátero (60º cada ángulo).
Por lo últimamente estudiado a simple vista vemos que el ángulo refracción es de 30º en toda la trayectoria interna del rayo.
La suma de los ángulos interiores es igual a la del exterior no adyacente: 60º = 30º + 30º.
Aplicamos lo de tantas veces: 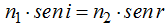
Sustituyendo valores y haciendo operaciones: