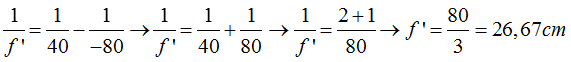Deducción de las fórmulas para resolver problemas de lentes
En la figura que tienes a continuación:
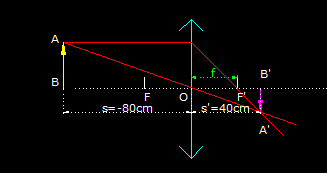
Los triángulos con fondo marrón vemos que son rectángulos. Si son semejantes, sus lados son proporcionales, es decir:
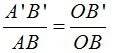
Las distancias AB y A’B’ representan al objeto y a su imagen.
Las distancias OB y OB’ representan a s y s’, respectivamente.
Por lo tanto, la proporción anterior podemos escribirla también:
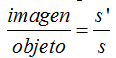
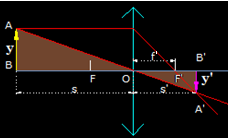
Analizando la figura siguiente ves que partimos con la misma figura anterior pero señalamos con una circunferencia el lugar donde vamos a realizar unos cálculos. A la derecha ampliamos la figura y fíjate que hemos señalado dos triángulos rectángulos con fondo azul:
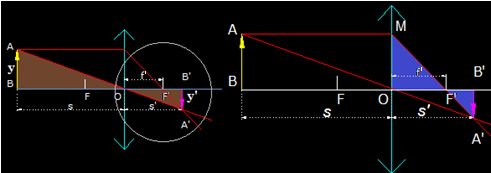
Los lados de estos triángulos son proporcionales por ser ambos rectángulos lo que quiere decir que:
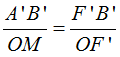
Si nos servimos de f’ distancia focal y s’ distancia de la imagen a la lente la proporción anterior podríamos haberla escrito:
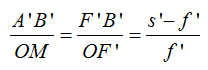
Anteriormente dedujimos: 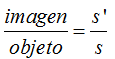 y formamos la proporción:
y formamos la proporción:
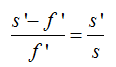
En el primer miembro de la igualdad, divido a cada término por su denominador, hago operaciones y simplifico:
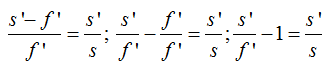
Ahora divido a cada término de la igualdad por s’, haciendo operaciones y transposición de términos llegamos a:
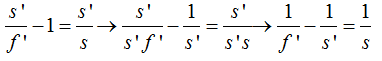
Haciendo transposición de términos obtengo: 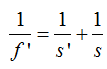
El valor de s que es la distancia del objeto a la lente se halla en “terreno” negativo porque corresponde, en un eje de coordenadas, al valor de la abscisa a la izquierda del 0 o centro óptico de la lente:
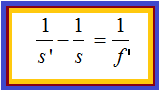
Debes poner mucho cuidado con los signos que debes asignar a cada dato cuando resuelves un problema.
Aplicamos en primer lugar a lentes convergentes:
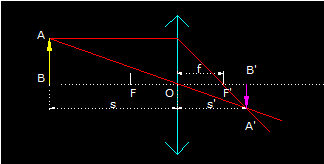
Vemos que la distancia focal f es positiva. La distancia s del objeto a la lente es negativa (izquierda del cero) y s’ la distancia de la lente a la imagen es positiva (derecha de cero).
5.48 Un objeto de 5cm de altura lo colocamos a 50cm sobre el eje de una lente convergente cuya distancia focal es de 20cm.
Presenta gráficamente su imagen y calcula su distancia al centro óptico.
Respuesta: 33,33cm
Lo dibujamos situando medidas con sus signos:
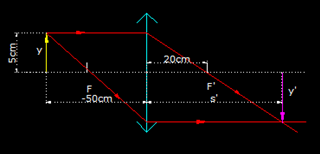
Aplicamos la fórmula sin tener en cuenta si nos referimos a lentes convergentes o divergentes y pondremos mucha atención en el momento de introducir los datos:
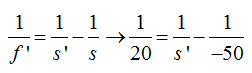
La última fracción del segundo término de la última igualdad puedo expresarla:
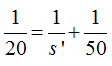
Haciendo operaciones y despejando a s’ llegamos a:
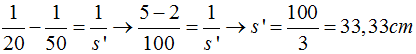
5.49 A 15cm delante de una lente convergente que tiene una distancia focal de 6cm colocamos un objeto. ¿A qué distancia de la lente se sitúa su imagen?
Respuesta: 10cm
Al ser igual al anterior omitimos figura y aplicamos directamente la ecuación fundamental de las lentes:
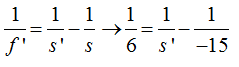
Hacemos operaciones y despejamos s’:
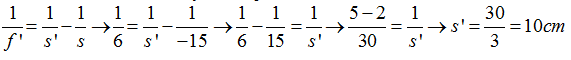
Aplicamos ahora a lentes divergentes:
Lo único que difiere a lo que acabas de estudiar es que el valor de es que en las lentes divergentes la distancia focal es negativa:
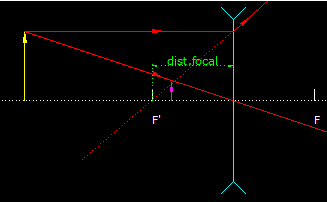
En una lente divergente la distancia focal se halla a la izquierda del centro óptico, por eso es negativa.
5.50 Colocamos un objeto de 9cm de altura a 20cm de distancia del centro óptico de una lente divergente y de 15cm de distancia focal. Calcula la distancia a la que se halla la imagen respecto al centro óptico de la lente y el tamaño de la misma.
Respuestas: -8,57cm y 3,856cm respectivamente.
A la figura le incorporamos los datos:
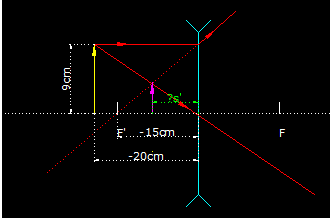
Calculamos el valor de s’.
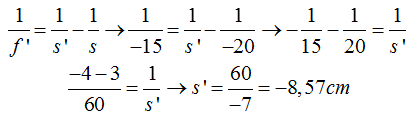
Para el tamaño recordamos lo estudiado con espejos esféricos:
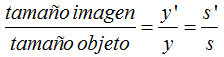
Sustituyendo valores y haciendo operaciones:
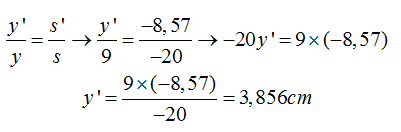
5.51 Calcula el tamaño y la distancia a la que aparece la imagen de un objeto de 10cm de altura situado a 60cm de una lente convergente cuya distancia focal es 20cm.
Respuestas: -5cm y 30cm respectivamente.
Solución
Lo hemos resuelto con otros datos por lo que se te facilitan resultados y figura:
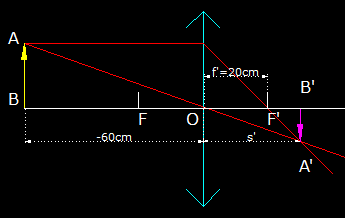
El signo (–) del tamaño de la imagen nos indica inversión (ordenada negativa).
5.52 ¿Cuánto vale la distancia focal de una lente convergente si sabemos que colocando un objeto a 80cm de ella, su imagen aparece a 40cm?
Respuesta: 26,67cm
Solución
Tomamos la misma fórmula: