Cociente de las distancias focales de un dioptrio esférico
Simplemente dividimos f entre f’ y simplificamos:
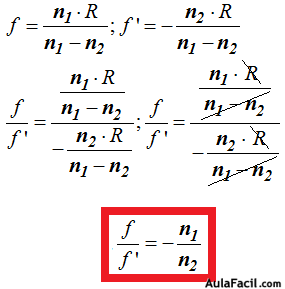
5.34 Las distancias focales de un dioptrio cóncavo son 10 y -16. Un medio es el aire ¿podrías decir cuánto vale n2?
Respuesta: n2 = 1,6
No tienes más que utilizar la última de las fórmulas deducidas:
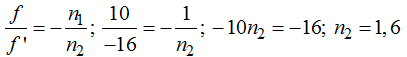
Aumento lateral de un dioptrio
En el caso del dioptrio es prácticamente lo mismo de lo estudiado en los espejos. Nos fijamos en la siguiente figura:
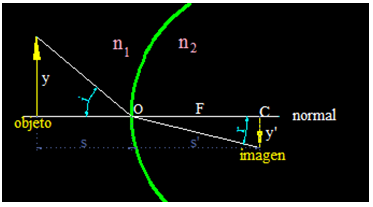
El eje de abscisas de un supuesto eje de coordenadas con centro en O vendría a ser la normal.
El rayo de luz incide con un ángulo i y se refracta con un ángulo r.
Las distancias del objeto e imagen al vértice del dioptrio miden - s y s’. No te olvides que s valor de la abscisa se halla a la izquierda del origen de coordenadas. El valor de s’ es positivo porque se halla a la derecha.
El signo de la medida de y es positivo porque las ordenadas sobre cero lo son, en cambio, y’ tiene valor negativo por hallarse bajo cero.
El valor de la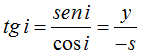 
El valor de la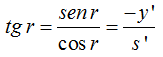 
Si dividimos ambas igualdades y hacemos operaciones teniendo cuidado de los signos:
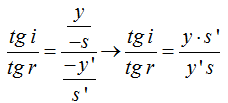
Como sabemos que los valores de los ángulos son pequeños podemos escribir:
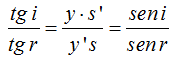(I)
Volvemos a utilizar la fórmula:
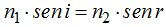
La convertimos en la proporción:
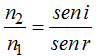
Producto de extremos igual al producto de medios.
Lo obtenido en (I) podemos completar:
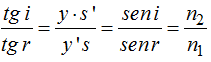
Sabemos que el aumento lateral es la relación entre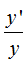 
.
De la última igualdad tomamos la proporción que nos interesa y hallamos los inversos del numerador y denominador por seguir el orden de subíndices.
Dejamos a y’ e y solas a la izquierda de la igualdad pasando al otro miembro sus factores correspondientes y llegamos a:
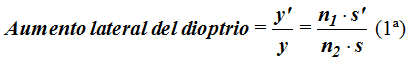(1ª)
Si quieres utilizar las distancias focales en lugar de los índices de refracción no tienes más que utilizar lo que dedujimos:
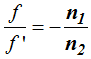en 
quedándonos la fórmula (y posiblemente vayan demasiadas):
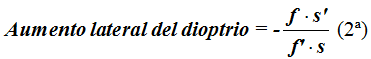(2ª)
