Momento de Inercia Rotacional - Repaso
Recordamos algo de lo que estudiamos anteriormente:
La distancia lineal (s) recorrida por un móvil entre un tiempo ti y un tiempo tf y la distancia angular recorrida por el mismo móvil en el mismo tiempo lo representamos con θ.
Gráficamente tendríamos:
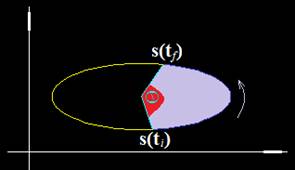
Recuerda que tenemos, respecto del ángulo, una velocidad angular ω, una aceleración angular α y en la línea del arco, una velocidad tangencial vt y una aceleración tangencial a.
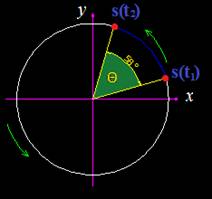
En esta figura el ángulo recorrido es θ y con línea azul el recorrido lineal efectuado por el móvil entre el tiempo t1 y en el momento t2.
La aceleración angular α es la misma para todas las partículas que componen el círculo.
La velocidad lineal, sin embargo, depende de la distancia que existe entre la partícula que consideramos y su distancia al eje de giro, es decir, del radio.
En la figura siguiente tomamos en cuenta 5 partículas, cada una a una distancia del centro de giro.
Cuanto más alejada del centro de giro se halle una partícula, mayor velocidad lineal adquiere:
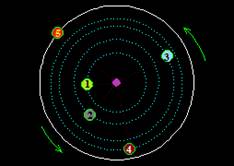
No te olvides que lo que no ha variado ha sido la aceleración angular.
Lo que sí ha variado es la velocidad lineal (en su circunferencia) de cada partícula. Cuanto mayor sea la distancia al centro, mayor será su aceleración.
La velocidad lineal depende del radio de cada partícula y por la aceleración angular que es igual para todas partículas.
Todo esto nos permite escribir:
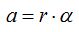
Pasemos a deducir la fórmula del momento de Inercia.
En la siguiente figura tienes una masa m que gira alrededor de un eje a una distancia r y la consideramos como una partícula de un cuerpo.
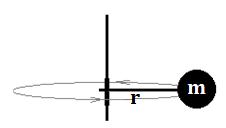
Sabemos que 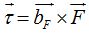 pero ahora nos interesan sus magnitudes por lo que escribiremos:
pero ahora nos interesan sus magnitudes por lo que escribiremos:
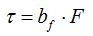
Esa fuerza que hemos de hacer equivale a la oposición que nos presenta el móvil, es decir, su Inercia.
La masa de la figura anterior cumple con 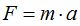
Dedujimos que: 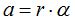
Sustituimos en 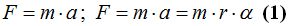
Sabemos que 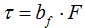 o que
o que 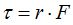 porque el brazo de la fuerza equivale al radio.
porque el brazo de la fuerza equivale al radio.
En 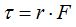 sustituimos a F por (1):
sustituimos a F por (1):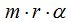 y obtenemos:
y obtenemos:
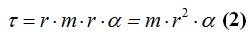
Conocemos también que: 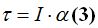
Igualamos los momentos que tenemos en (2) y (3) simplificando:
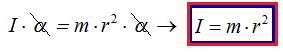
Este sería el caso de una partícula pero ¿cómo expresamos la fórmula para un sistema de partículas?
Sencillamente valiéndonos del signo de la sumatoria que lo vimos anteriormente:
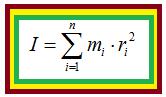
Esta fórmula nos permite el cálculo de algunos problemas que vamos a resolver a continuación.
