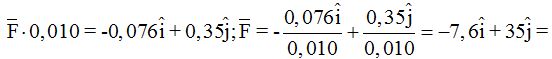Impulso en dos direcciones
Hasta ahora hemos considerado impactos horizontales o verticales, es decir, el móvil se acerca al suelo o pared horizontalmente y sale rebotado en la misma dirección y sentido contrario.
Podemos contemplar que no siempre sucede así. La llegada del móvil a la pared o al suelo puede producirse bajo un ángulo.
Si el objeto que choca contra la pared o suelo rebota lo más probable es que salga despedido con una dirección diferente al de la llegada:

En la figura apreciamos el impacto contra el suelo de la pista de una pelota de tenis obtenida con el “ojo de halcón”.
Si observas, la dirección de llegada la hace bajo un determinado ángulo y el rebote se produce sobre el mismo ángulo u otro diferente pero en distinta dirección.
En este tipo de problemas has de tener presente que la velocidad de llegada y la de salida tras el impacto, están representadas por magnitudes vectoriales.
Lo normal es que tengas que hacer uso de las componentes del vector velocidad.
Tendrás la necesidad de aplicar los vectores unitarios que te serán de gran utilidad a la hora de plantear ecuaciones y concretar resultados.
Como hemos hecho en otros casos vamos a estudiar este tema con casos prácticos.
2.189 Nuestro conocido Bart Simpson recibe un balón de 300 g horizontalmente a 15m/s y lo despeja formando un ángulo de 60º a 30m/s:
El contacto del balón con el pie ha durado 0,01 segundos.
1: ¿Cuánto vale el Impulso de la fuerza ejercida por el pie sobre el balón.
2: ¿Cuánto vale la Fuerza media que Bartolomé ha aplicado al balón?
Respuestas: 1) 11,91 kg.m/s; 2) 1191 N
Solución
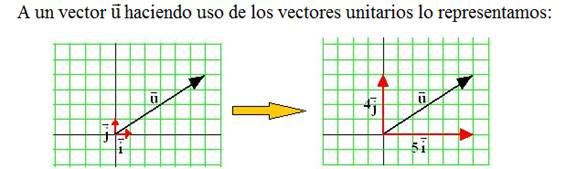
Dibujamos un sencillo esquema sobre un eje de coordenadas en el que vemos la llegada del balón horizontalmente respecto del suelo con una velocidad de 15m/s y después del pateo que dura 0,01 s sale con un ángulo de 60º hacia arriba y derecha a 30m/s:
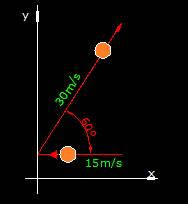
La velocidad de llegada es un vector que como puedes ver se dirige hacia la izquierda.
A este vector si queremos descomponer en sus componentes, vemos que la vertical es cero o no existe.
La horizontal tiene negativo su vector unitario por lo que escribimos:
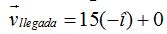 .
.
Ahora analizamos las componentes del vector velocidad de salida:
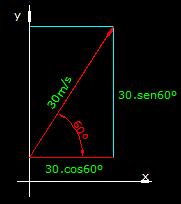
La suma de las componentes horizontal y vertical nos dará el valor de 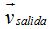 cuyo módulo vale 30:
cuyo módulo vale 30:
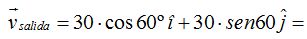
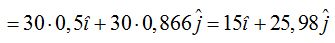
Hallamos la variación de la cantidad de movimiento o Impulso:
Sabemos que p2 – p1 = m2.v2 – m1v1
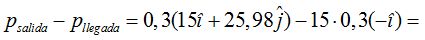
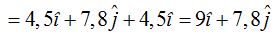
El Impulso = 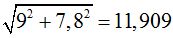 kg.m/s
kg.m/s
La Fuerza media utilizada en el pateo nos vendrá dada por:
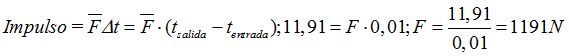
Nota: A la fuerza (F) le colocamos una pequeña raya horizontal en lugar de una flecha para indicar que se trata de la fuerza media (en el tiempo que dura el impacto).
2.190 Resuelve el siguiente problema del niño jugando al tenis con los datos siguientes:

La pelota de tenis de peso 56 gramos se desplaza a una velocidad de 8m/s con un ángulo de 30º cuando impacta contra el suelo durante 10 milisegundos y después del bote sale despedida con un ángulo de 22º y a una velocidad 6m/s.
Calcula la fuerza con la que el suelo de la pista reacciona sobre la pelota.
Respuesta: 35,81 N
Solución
Tras admirar el buen estilo del simpático tenista que sin duda se entrena para partidos de larga duración (alimentación asistida) es importante que hagamos un dibujo en el que aparezcan todos los detalles esenciales que correspondan al contenido del texto del problema.
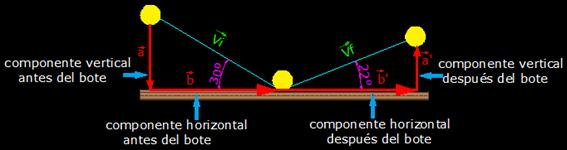
Ten en cuenta que las velocidades que nos dan son cantidades vectoriales ya que nos indican su dirección.
Sabemos de Matemáticas que la suma de vectores podemos escribir:
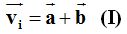
Las componentes de 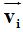 son:
son:
La vertical 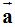 cuyo sentido es negativo (el valor del eje de ordenadas es descendente) y la horizontal
cuyo sentido es negativo (el valor del eje de ordenadas es descendente) y la horizontal 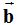 con sentido positivo.
con sentido positivo.
Volvemos a utilizar los vectores unitarios:
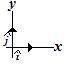
Haciendo uso de la Trigonometría vemos que
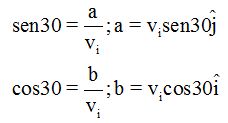
Sustituimos estos valores en (I):
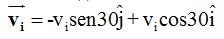
Las componentes de 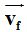 son:
son:
La vertical 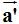 y
y 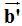 en ambos casos con sentidos positivos.
en ambos casos con sentidos positivos.
El ángulo mide 22º y haciendo lo mismo de lo realizado con el vector de llegada tenemos:
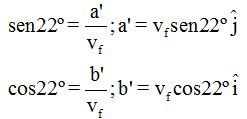
Como 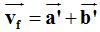 sustituimos estos valores por los que acabamos de deducir:
sustituimos estos valores por los que acabamos de deducir:
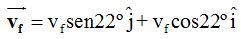
Que nos permite escribir en la fórmula:
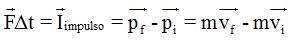
donde sustituimos los valores de 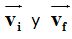 :
:
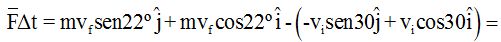
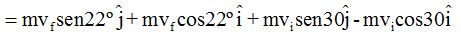
Sustituimos m, vi y vf , senos y cosenos de los ángulos por sus valores y el peso de la pelota la escribimos en kg :
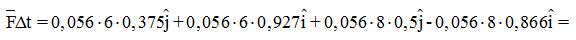
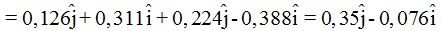
Sabemos que el choque ha durado 10 milisegundos que lo sustituimos en Δt: