Equivalencias entre ambas asociaciones
Relacionar estas dos asociaciones es importante en muchos casos.
Procura entender bien y verás que no es difícil.
Para que las asociaciones sean equivalentes nos deben dar resultados iguales.
Podemos encontrarnos con una asociación de Resistencias en estrella pero puede convenirnos transformarla en triángulo o viceversa.
Supongamos que tenemos una asociación en triángulo cuyas Resistencias conocemos Ra, Rb y Rc y necesitamos calcular las Resistencias R1, R2 y R3 (en estrella).
A una asociación en triángulo le corresponde su equivalente en estrella y para relacionarlas vamos a efectuar los pasos siguientes:
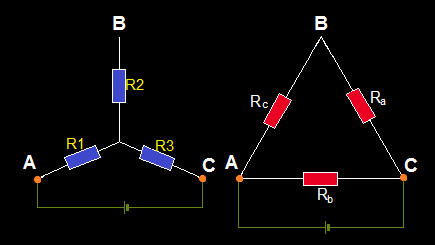
1.- Dibujamos ambas asociaciones por separado:
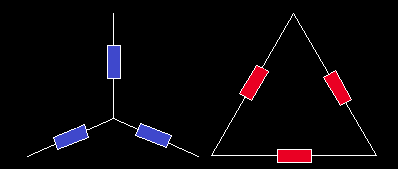
2.- Ponemos nombres a los vértices del triángulo:
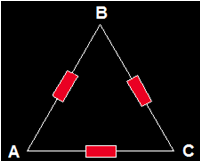
3.- Ponemos nombres a las Resistencias de esta asociación con relación al nombre del vértice opuesto:
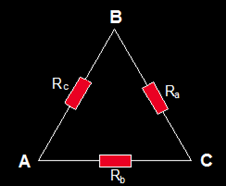
4.- Ponemos nombre a las Resistencias en estrella:
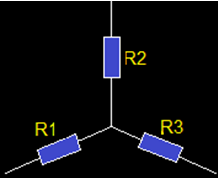
5.- Superpongo las dos asociaciones de modo que el vértice A es el final de la R1, el vértice B conecta con la Resistencia R2 y R3 con el vértice C:
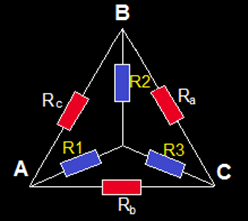
6.- Para que estos dos circuitos sean equivalentes es necesario que la Resistencia resultante entre los vértices A y B tengan el mismo valor en ambas asociaciones.
Lo mismo cabe decir para las Resistencias resultantes entre los vértices B y C y entre C y A.
7.- Establecemos conexión desde una fuente tomando como puntos receptores de la corriente únicamente los finales de las Resistencias R1 y R2
En este caso, no tenemos en cuenta la asociación en triángulo.
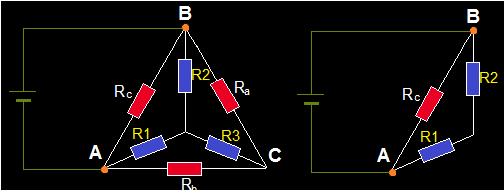
La Resistencia R3 está fuera de conexión.
8- Vemos que R1 y R2 están en serie y ambas en paralelo con Rc:
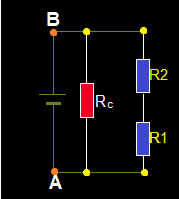
9.- El valor de la Resultante de las Resistencias que proceden de la asociación en estrella la representamos con RAB por estar en serie es: RAB = R1 + R2.
10.- Analicemos lo que sucede con la asociación en triángulo. No tenemos en cuenta la asociación en estrella. Seguimos con los puntos A y B conectados a la fuente:
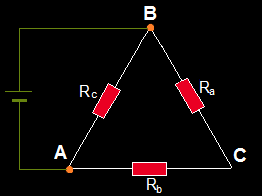
Ra y Rb están en serie y en paralelo con Rc:
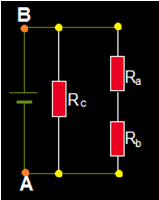
11.- Llamando RAB a la resultante tenemos:
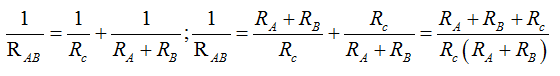
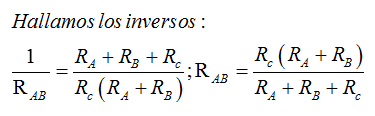
12.- Observa que hemos obtenido, por un lado, RAB = R1 + R2 y por otro,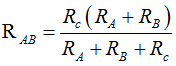 
y hemos dicho que para que haya equivalencia estas Resistencias resultantes han de tener el mismo valor, es decir:
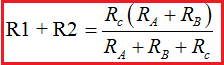
13.- Repetimos este análisis, ahora con lo que sucede entre los vértices B y C y en el que lo único que varían son los nombres de los elementos.
Primero analizamos lo que se refiere a la parte de la asociación en estrella.
A la Resistencia resultante entre los vértices B y C la llamamos RBC.
Las Resistencias R2 y R3 están en serie por lo que:
RBC = R2 + R3
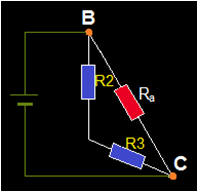
14.- Analizamos lo que sucede con la formación en triángulo:
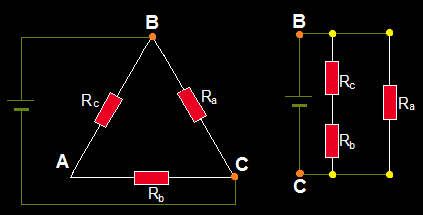
Rc y Rb se hallan en serie y su resultante en paralelo con Ra.
La resultante de este sistema que lo representa RBC será:
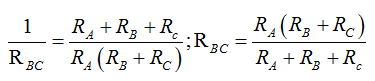
Anteriormente calculamos que RBC = R2 + R3, por lo que:
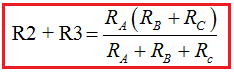
15.- Siguiendo este mismo proceso y tomando los puntos A y C como receptor y salida de corriente vemos en la figura siguiente que en la asociación en estrella las Resistencias R1 y R3 están en serie y llamando RAC a la resultante tendremos:
RAC = R1 + R3
En la asociación en triángulo las que se hallan en serie son Ra y Rc y ésta resultante en paralelo con Rb.
La resultante de la asociación en triángulo es:
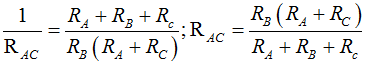
Como RAC también es igual a R1 + R3 podemos escribir:
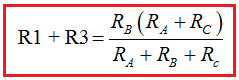
16.- A partir de este momento hay tres ecuaciones con 3 incógnitas R1, R2 y R3 que las hemos colocado en recuadros rojos:
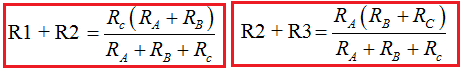
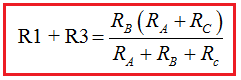
Tenemos el sistema de ecuaciones:
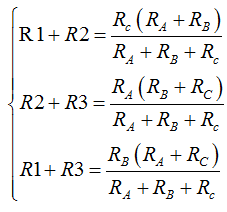
Seguramente aparenta lo que no es. No es nada complicada la resolución si te fijas un poco, tomas las dos primeras ecuaciones cambiando de signo a la segunda:
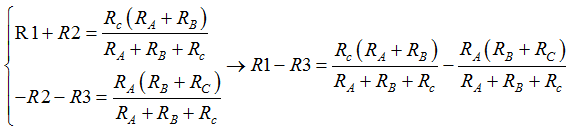
Quitamos paréntesis:
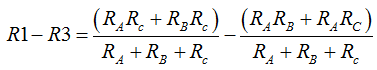
Como tienen los mismos denominadores sumamos los numeradores teniendo cuidado con el cambio del signo cuando éste está delante de un paréntesis y es negativo. Reduciendo términos semejantes obtenemos:
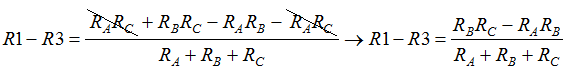
Ahora podemos sumar esta ecuación con la 3ª:
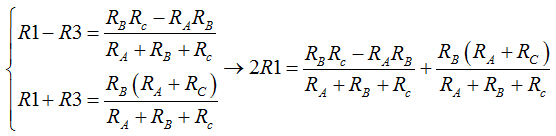
Quitamos paréntesis y al tener iguales los denominadores los podemos sumar reduciendo los términos semejantes:
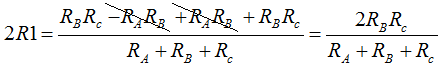
simplificando por 2 en ambos lados de la igualdad: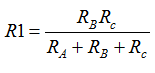 
Ahora calculamos R2 haciendo operaciones paso a paso tienes:
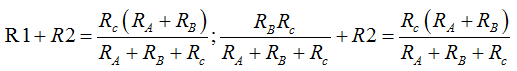
Hemos hecho la sustitución de R1 por el valor que hemos hallado.
Realizamos operaciones a partir de esta última igualdad llegamos a:
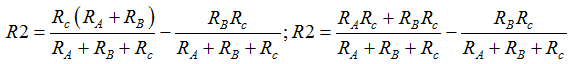
Restamos y reducimos términos semejantes:
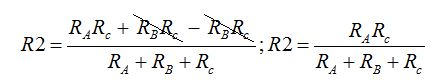
Los cálculos para conocer el valor R3 los tienes a continuación. Partimos de:
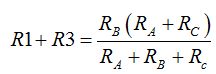
Sustituimos el valor de R1:
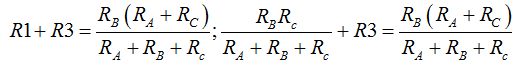
Hacemos operaciones:
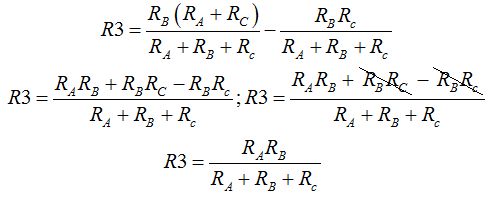
Los valores de las Resistencias en la asociación en estrella a partir de las asociadas en triángulo son:
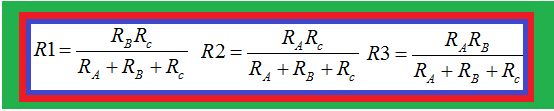
Ahora vamos a hacer la transformación contraria, es decir, conocemos los valores de las Resistencias en estrella y calculamos sus equivalentes en la asociación en Delta o triángulo.
El sistema de ecuaciones que se nos presenta es:
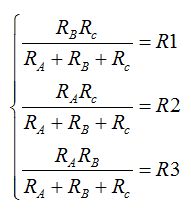
Cuando un sistema ves que no te convence utilizar cualquiera de los tres métodos tradicionales como en el sistema:
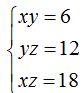
lo más sencillo es multiplicar todos los términos de cada lado del signo igual y obtienes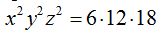 
.
Ahora divides este resultado por una de las ecuaciones, tomamos la 1ª:
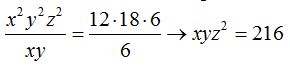
Hacemos lo mismo con la 2ª ecuación:
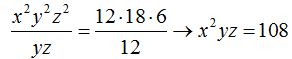
Dividimos ambas ecuaciones y hacemos simplificaciones:
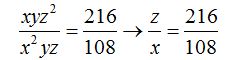
Despejamos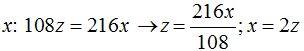 
Este valor lo sustituimos en la 3ª ecuación y obtenemos:
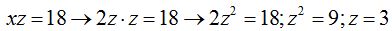
Conocido el valor de una incógnita las demás se calculan fácilmente:
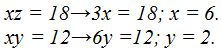
Hay varias formas de resolver un sistema de ecuaciones.
¿Cómo resolvemos el sistema:
?
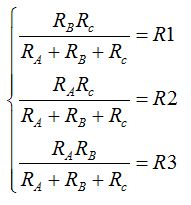Recuerda que a la izquierda del igual se hallan los valores desconocidos y a la derecha los que conocemos.
Multiplicamos la 1ª ecuación por la 2ª:
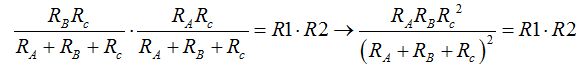
Ahora multiplicamos la 2ª por la 3ª:
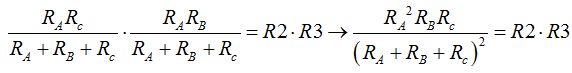
Y por fin, multiplicamos la 1ª por 3ª ecuación:
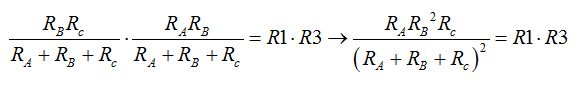
Observa que todos los denominadores son iguales.
Sumamos las expresiones situadas a uno y otro lado del signo igual:
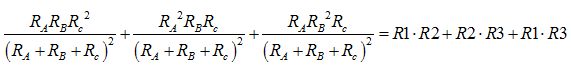
Al ser el mismo denominador en cada fracción sumamos los numeradores permaneciendo el denominador común:
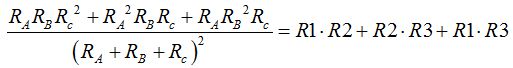
En el numerador del primer miembro de la igualdad podemos sacar factor común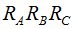 
y la ecuación nos queda:
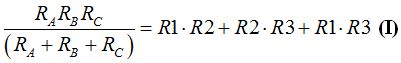
Dividimos esta ecuación por la 1ª:
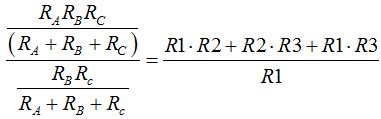
Simplificamos el primer miembro:
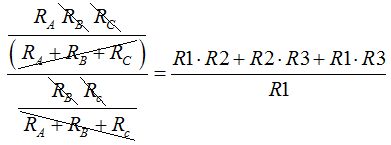
Nos ha quedado:
Calculamos el valor de RB y para ello dividimos la expresión (I) por la 2ª ecuación y realizando los mismos pasos para el cálculo de RA llegamos a:
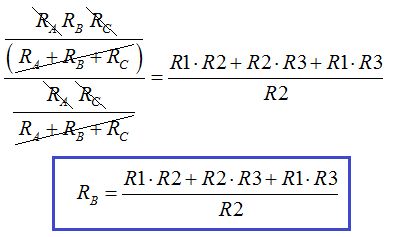
Realizamos los mismos pasos para el cálculo de Rc:
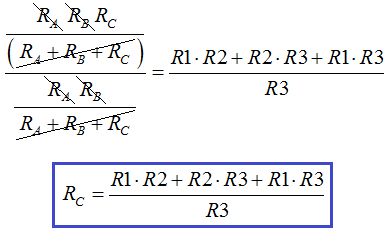
Es cierto que te puede resultar largo el proceso pero resulta fácil y hasta divertido (en cálculos un poco largos nunca tengas prisas).
