Equivalencias entre ambas asociaciones - Ejercicios
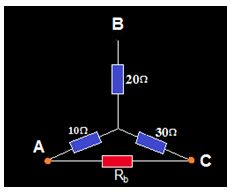
7.12 Tenemos la asociación en estrella siguiente:
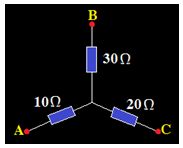
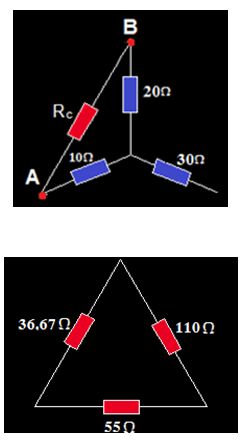
Calcula su equivalente en triángulo.
Respuesta: RA = 110Ω; RB = 55Ω; RC =36,67Ω
Aplicamos las fórmulas que hemos deducido:
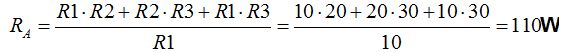
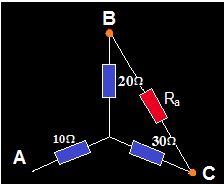
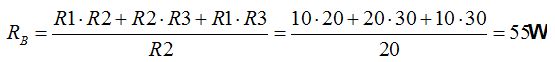
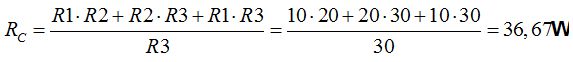
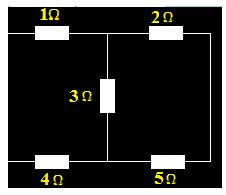
7.13 ¿Cuál es la resistencia equivalente a las que tienes en la figura siguiente?
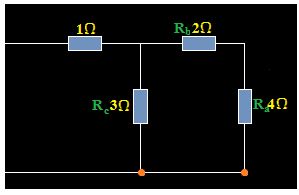
Respuesta: 1,62Ω
Las Resistencias de 2, 3 y 4kΩ están en triángulo. Observa:
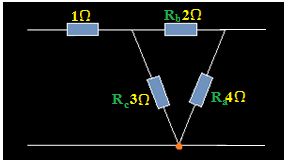
Si tenemos alguna dificultad para el cálculo dibujamos su equivalente en estrella:
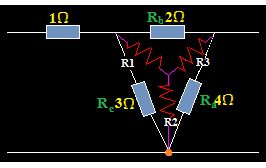
Calculamos las Resistencias R1, R2 y R3 conectadas en estrella.
Aplicamos lo estudiado:
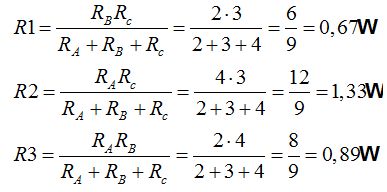
El esquema primitivo, al final nos queda:
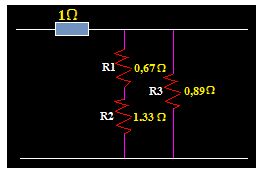
La Resistencia equivalente a las dos en serie R1 y R2 con R3 es:
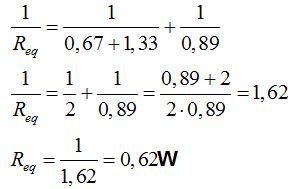
La Resistencia final es la que acabamos de obtener más la Resistencia de 1Ω que la tenemos en serie y que estará aburrida por no haber intervenido hasta ahora:
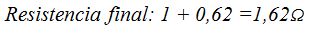
7.14 Calcula la Resistencia equivalente a las que figuran en el circuito siguiente:
Respuesta: 1,43Ω
Solución.
Lo modificamos:
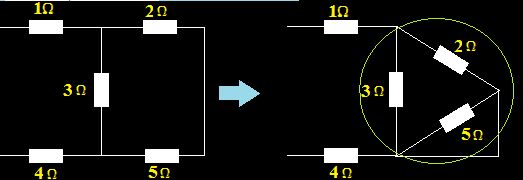
Pasamos de triángulo a estrella:
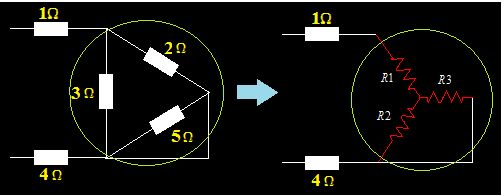
Calculamos los valores de R1, R2 y R3:
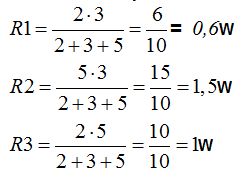
Volvemos a modificar con los datos obtenidos el último esquema:
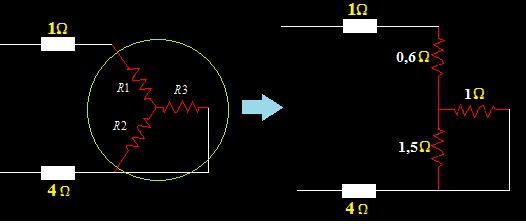
Tenemos en serie las Resistencias: 1Ω + 0,6 Ω= 1,6 Ω
También 4Ω + 1,5Ω = 5,5Ω
Estas dos Resistencias están en paralelo y su equivalente con la Resistencia de 1Ω que está en serie es:
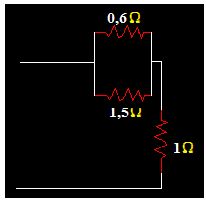
Calculamos la Resistencia equivalente (Requiv) de las que se hallan en paralelo:
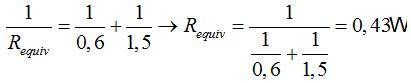
La Resistencia Total del circuito es: 0,43Ω + 1Ω = 1,43Ω
