Velocidad instantánea y su módulo
En el momento que el intervalo del tiempo tiende a cero podemos referirnos a la velocidad instantánea y la representamos del modo siguiente:
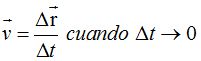
Pero sucede que cuando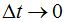 
el valor de 
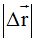coincide con 
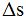según hemos visto por lo que podemos decir que también:
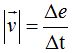
En este caso, el módulo de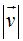 
equivale a la rapidez.
Cuando hablamos de velocidad nos referimos al vector velocidad instantánea.
1.70 Un móvil da una vuelta al circuito rectangular que tienes a continuación:
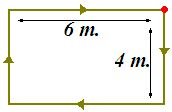
en 5 segundos saliendo del punto rojo y llegando al mismo lugar.
1.- Calcula el espacio recorrido
2.- El vector de desplazamiento
4ª.- El vector velocidad media
Respuestas: 1ª 20 m.; 2ª 0 m.; 3ª 4 s.; 0 m.
Solución
El perímetro del rectángulo es de 20m.
El valor absoluto del vector desplazamiento vale 0 m. porque su punto inicial y final es el mismo.
La rapidez media nos viene dada por el cociente del camino que ha recorrido el móvil y el tiempo empleado, es decir,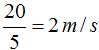 
.
El valor del vector velocidad media como nos viene dado por el cociente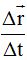 
y el numerador vale 0 su cociente también tendrá este valor.
LA VELOCIDAD INSTANTÁNEA EN UN PUNTO COMO LÍMITE DE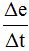 
CUANDO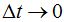 
Sabemos que el espacio a recorrer está en función del tiempo, es decir, cuanto más tiempo estás caminando, mayor será el camino recorrido por lo que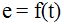 
.
Haciendo uso de lo estudiado en matemáticas en lo que se refiere a límites puedo escribir que la velocidad instantánea en un punto lo escribo:
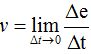
En un eje de coordenadas el eje de abscisas representa los valores del tiempo y el de ordenadas los espacios:
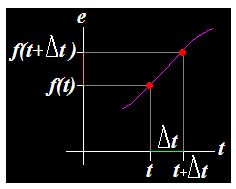
En un momento dado, cuando el tiempo señala t (eje de abscisas) el punto correspondiente de la función corresponde a f(t) (eje de ordenadas).
Incrementamos el tiempo en Δt (color verde eje de abscisas) con lo que su valor correspondiente en la función es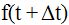 
(color naranja eje de ordenadas).
La velocidad instantánea nos viene dada por el cociente del espacio recorrido entre los tiempos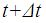 
y t , es decir, 
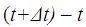que corresponden a menos cuando el que lo escribimos:
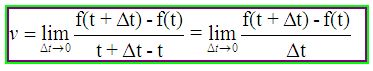
1.71 Sabiendo que el espacio recorrido está en función del tiempo, ¿cuál es la velocidad instantánea (en función del tiempo) de un móvil cuyo movimiento corresponde a la ecuación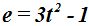 
?
Respuesta: 6t
Solución.
Una vez que hayas entendido perfectamente la deducción de la fórmula anterior, no tienes más que aplicarla:
Sustituyes los valores que conoces, teniendo en cuenta que t se halla elevada al cuadrado y multiplicada por 3:
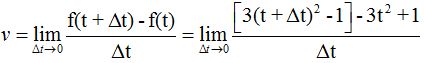
Hacemos operaciones dentro de los corchetes:
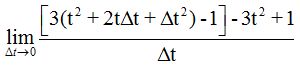
Eliminamos los corchetes y reducimos términos semejantes:
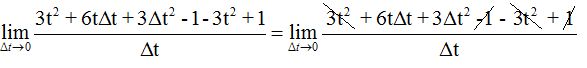
Nota. No elimines los términos que contengan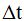 
por tender a 0 porque puedes crear indeterminaciones.
Antes de tomar límites dividimos todos los términos por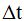 
:
Nos queda:
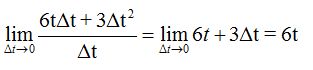
El concreto valor de t multiplicado por 6 nos da la velocidad del móvil en ese instante.
1.72 Sabiendo que el movimiento de un móvil corresponde a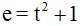 
calcula la velocidad instantánea (en m.) cuando t = 3 s.
Respuesta: 6m/s.
Solución.
Las operaciones a realizar paso a paso son:
1.73 El vector de posición de un móvil es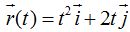 
Cuáles son el vector velocidad instantánea y su módulo cuando t vale 5 s?
Respuestas: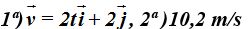 
Solución.
Tenemos un vector de posición (en función del tiempo) que nos han dado:
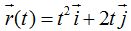
Incrementamos el tiempo t en una cantidad muy pequeña Δt que tiende a 0.
Dado que hemos incrementado (aunque sea un infinitésimo) el tiempo tenemos un nuevo vector de posición: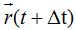 
que equivale a: 
.
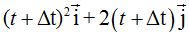Como ves, en este caso, no hemos hecho nada más que sustituir t por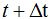 
.
Sabemos que la velocidad media entre los momentos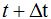 
y t lo podemos escribir:
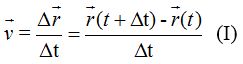
Sabemos que el vector de posición después del incremento del tiempo es: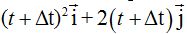 
y antes del incremento: 
.
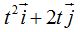por lo que:
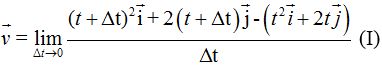
Haciendo operaciones tenemos:
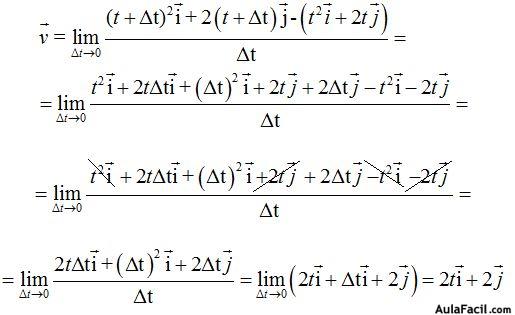
Hemos dividido a cada sumando del numerador por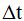 
antes de tomar límites para evitar indeterminaciones como 
.
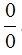Una vez obtenida la primera respuesta no tienes más que sustituir t por 5 (módulo del vector velocidad del móvil en el segundo 5):
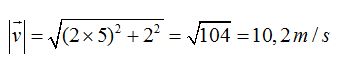
EL VECTOR DE LA VELOCIDAD INSTANTÁNEA ES TANGENTE A LA TRAYECTORIA.
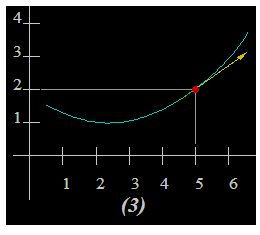
Podemos demostrar que el vector velocidad es tangente a la trayectoria del siguiente modo:
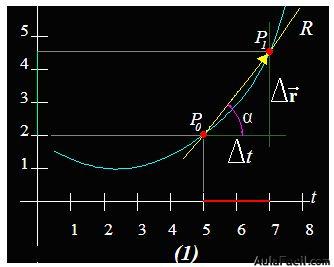
En la figura vemos en azul la trayectoria a recorrer por el móvil.
En el eje de ordenadas ves las posiciones P0 y P1 que ocupa el móvil en los segundos 5 y 7, respectivamente situados en el eje de abscisas.
El vector de desplazamiento está situado en la recta R que como ves, es secante en los puntos P0 y P1, formando un ángulo α con la paralela al eje x.
Los incrementos de tiempo y posición nos vienen dados por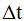 
= (7 - 5) para el tiempo y 
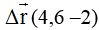para el vector de desplazamiento.
A medida que disminuimos el valor del incremento del tiempo, los puntos de los vectores de posición se aproximan como podemos comprobar en la siguiente figura:
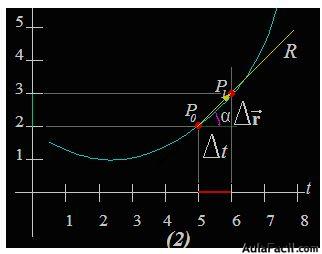
Como ambos incrementos han disminuido sus valores, el valor del ángulo disminuye.
El cateto opuesto al ángulo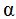 
es 
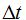y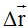 
el contiguo. Sabemos que la tangente de un ángulo es igual al cociente del cateto opuesto 
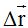dividido por el cateto contiguo 
:
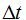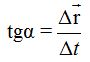
Cuando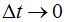 
, es decir, el incremento del tiempo es un infinitésimo nos hallamos en que los puntos P0 y P1 se juntan formando uno solo que corresponde al lugar en que el vector de la velocidad instantánea se ha convertido en una recta tangente a la trayectoria:
