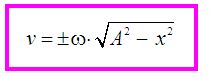Velocidad en el movimiento armónico simple
La velocidad la podemos expresar en función del tiempo y a partir de aquí, en función de la elongación (x).
Sabemos que la función que se deriva del espacio (x) en función del tiempo (t) es la velocidad:
Partimos de: 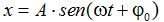
Derivando ambos miembros de la igualdad en función de t:
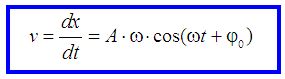
En el caso de que hubiésemos partido de: 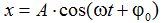
La velocidad la calculamos:

Ahora vamos a deducir la fórmula que nos permita calcular la velocidad en función de la elongación.
Partimos de:
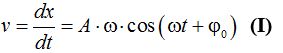
Sabemos por lo estudiado en Trigonometría: 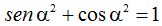
Lo aplicamos en este caso haciendo:
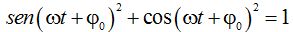
Despejamos 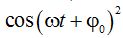 :
:
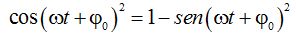
Hallamos la raíces cuadradas en ambos miembros:
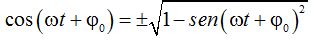
Este valor lo sustituimos en (I):
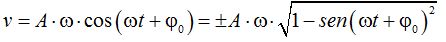
Introducimos A dentro de la raíz:
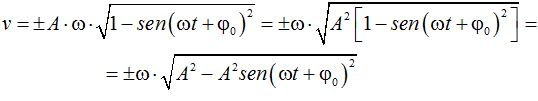
Si te fijas:
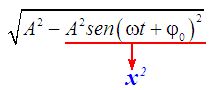
Podemos escribir la fórmula de la velocidad: