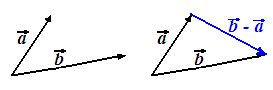Vectores unitarios
Los vectores unitarios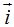 
y 
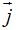decimos que son unitarios porque su módulo vale 1.
Cualquier vector puedes escribirlo sirviéndote de los vectores unitarios como lo verás en seguida.
En la figura siguiente tienes representados los vectores unitarios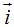 
y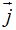 
:
Si analizas el vector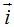 
, ves que su módulo se encuentra sobre el mismo eje de abscisas, esto quiere decir que uno de sus componentes, en este caso el relativo al eje de ordenadas vale 0 y el otro, necesariamente debe valer 1 para que su módulo valga 1:
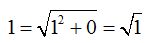
El vector unitario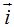 
corresponde al punto = ( 1, 0)
En cuanto al vector sucede que el valor 0 está situado sobre el eje de abscisas y 1 sobre el eje de ordenadas (última figura) para que su módulo sea 1:
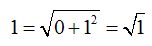
El vector unitario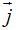 
corresponde al punto = ( 0, 1).
1.56 Representa en un eje de coordenadas el vector 4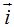
Respuesta:
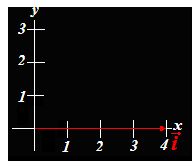
Solución.
Se reduce a un simple producto: cuatro veces el vector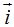 
= 4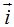
Nos ha quedado como resultado el vector 4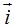
1.57 Representa en un eje de coordenadas el vector 3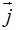
.
Respuesta:
1.58 Representa en un eje de coordenadas la suma de los vectores anteriores: 4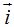
+ 3 
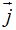
Respuesta:
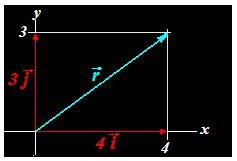
Solución.
Hemos sumado los vectores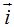 
y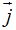 
obteniendo como resultado de la suma el vector 
.
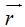Sabemos que para sumar dos vectores:
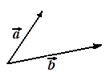
puedes hacer trazando las paralelas de cada vector y la diagonal del paralelogramo que se nos ha formado será el vector de la suma:
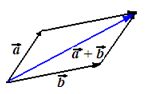
La suma de dos vectores
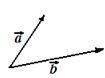
también lo obtenemos de hacer coincidir el origen de uno con el final del otro:
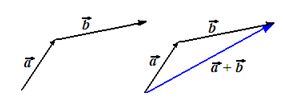
Un modo sencillo para restar vectores es sumar uno de los vectores con el opuesto del otro.
Dos vectores son opuestos si sus sentidos son diferentes coincidiendo en dirección y módulo.
Ejemplo:
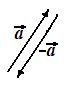estos dos vectores son opuestos.
Para restar
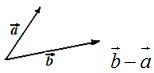puedes sumar al vector 
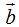el opuesto de 
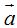, es decir:
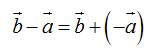
Gráficamente lo representamos:
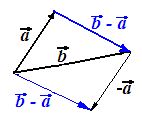
Del extremo del vector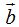 
sumamos el vector 
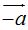y uniendo el origen con el extremo de este último vector obtenemos el vector de la diferencia.
El resultado de la diferencia de los vectores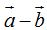 
sería:
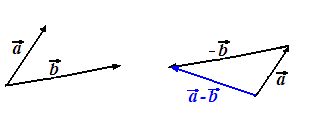
Un modo muy sencillo de representar gráficamente la diferencia de dos vectores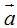 
y 
, 
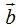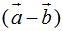es:
Trazar, directamente, un vector cuyo origen se encuentra en el extremo de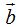 
(sustraendo) y su extremo en el extremo de 
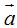(minuendo):
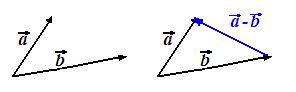
Del mismo modo: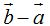 
lo haríamos directamente:
