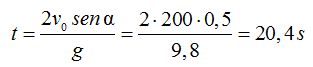Ecuaciones de la velocidad y de la posición de un móvil en el movimiento parabólico
Cálculo de la velocidad:
En la figura siguiente es conveniente te fijes en los puntos que vamos a tratar:
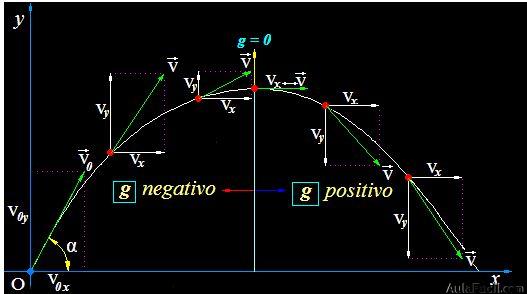
El vector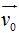 
nace en el origen de coordenadas, es la resultante de dos velocidades 
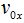(horizontal) y 
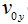(vertical).
Es importante fijarse en el ángulo α porque si lanzamos un objeto con un determinado ángulo, tanto la altura máxima obtenida en su trayectoria como la distancia horizontal alcanzada van a depender, en parte, del valor de dicho ángulo.
El valor de α lo calculamos teniendo en cuenta las componentes. Vemos por la última figura (tomando el valor del módulo del vector:
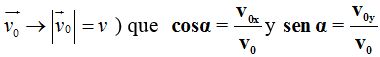
Despejando las componentes:
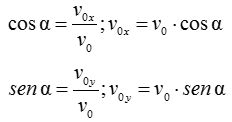
Si te fijas en la figura última, la velocidad horizontal es siempre constante (vx).
En cambio, la velocidad vertical disminuye a medida que pasa el tiempo por efecto de la atracción de la Tierra en la mitad del recorrido, mientras sube. Cuando desciende se acelera positivamente por efecto de la gravedad (g).
Debes verificarlo mediante la observación.
Habrá un momento en el que g vale cero (centro de la trayectoria). En este caso no hay componente vertical y la resultante coincide con vx.
En el caso de que el móvil se halle en su movimiento ascendente, es decir, cuando g es negativa, en un momento t su velocidad nos vendrá dada por: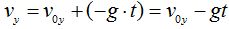 
La velocidad resultante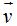 
no olvides que es la suma vectorial de 
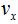y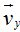 
que nos permite escribir: 
.
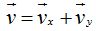También podemos escribir: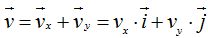 
y de esta última igualdad calculamos el módulo de 
:
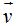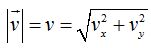
Cálculo de la posición:
Es suficiente que tengas presente que la velocidad horizontal es uniforme, no varía.
La velocidad vertical es uniformemente acelerada.
Teniendo en cuenta estos dos detalles tendremos que para dar la posición del móvil necesitamos conocer el punto donde se halla, es decir, el punto que nos vendrá dado por las coordenadas (x,y).
El valor de x lo obtenemos de aplicar:
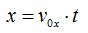
El valor de y lo obtenemos de aplicar:
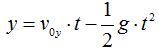
El vector de posición nos viene dado por la suma vectorial de los vectores de posición que representan a cada componente:
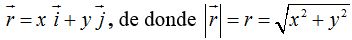
PRÁCTICA: TRAYECTORIA PARABÓLICA COMPLETA
En este caso, la trayectoria parabólica tiene la forma:
En la práctica, en un elevado porcentaje, los cálculos van encaminados a conocer:
A) Tiempo en el que el móvil permanece en movimiento
B) Distancia horizontal recorrida por el móvil o alcance
C) Altura máxima alcanzada en su trayectoria.
A) Tiempo en el que el móvil permanece en movimiento
El tiempo que dura el movimiento parabólico completo de un móvil lo podemos calcular de un modo muy sencillo.
En su día estudiamos en el movimiento rectilíneo uniformemente variado que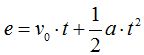 
.
Aplicando al movimiento parabólico el espacio (e), su componente, referida al eje de ordenadas (y) vale 0 porque sale del nivel 0 para llegar a este valor (nos estamos refiriendo al movimiento parabólico completo).
Por otra parte, la aceleración equivale a la atracción de la Tierra en ese lugar (g) que es negativo.
Teniendo en cuenta estos detalles tendremos que:
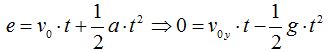
A cada término de la última igualdad puedes dividirlo por t que tiene un valor determinado y sabemos que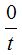 
vale 0 por lo que:
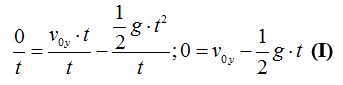
Con anterioridad recordarás que dedujimos el valor de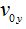 
y que es:
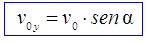
Lo sustituimos en (I):
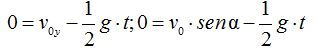
Esta última igualdad podemos escribirla:
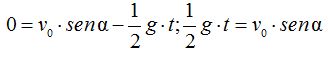
Despejamos el valor de t:
1.123 Supongamos que el señor Picapiedra es capaz de dar un golpe a la pelota de golf capaz de adquirir ésta una velocidad de 200 m/s.
¿Cuánto tiempo permanecerá en el aire si sale con un ángulo de 30º?
Respuesta: 20,4 s
Solución.
Aplicamos la última fórmula deducida y sustituimos valores que conocemos sabiendo que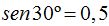 
:
