Desfase
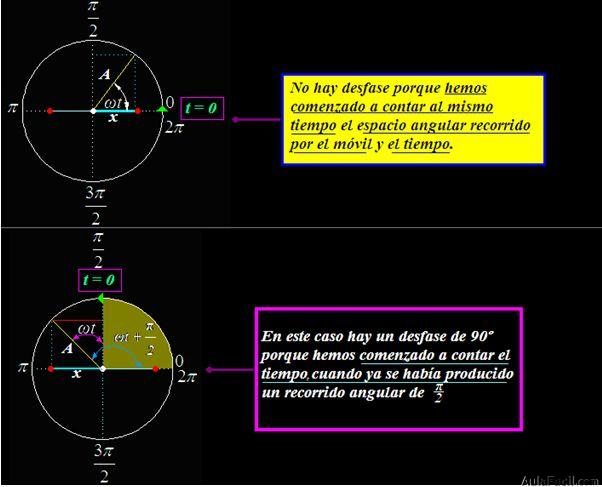
Cuando el punto donde comenzamos a medir el tiempo no coincide con el punto donde comenzamos a medir el espacio angular recorrido por el móvil, se produce un desfase.
Observa las dos últimas figuras:
La elongación (x) podemos representarla verticalmente y en la gráfica siguiente puedes comprobar:
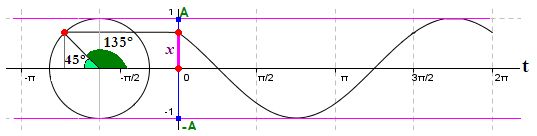
dicha representación y ves el lugar donde hemos representado al tiempo.
Cuando el tiempo vale 0 o cuando comenzamos a contar el valor de éste, el móvil ya se había desplazado 135º.
Lo mismo cabe decir en el caso de la figura siguiente:
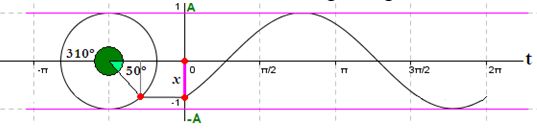
Al ángulo recorrido por el móvil antes de comenzar a contar el tiempo lo representamos por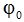 
.
Aclaremos bien la idea de la elongación realizando unos ejercicios, pero antes:
¿Qué fórmula uso: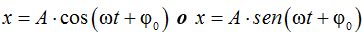 
?
Dijimos anteriormente que lo que las diferencia a ambas es un ángulo de fase inicial equivalente a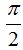 
y aunque sea volver a repetir tienes a continuación la figura a modo de resumen:
Si el movimiento comienza a partir del punto de equilibrio, por comodidad puedes utilizar la función seno.
Si el movimiento comienza a partir de los extremos, por comodidad puedes utilizar la función coseno.
1.133 Un movimiento armónico simple nos viene dado por la ecuación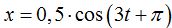 
.
Calcula:
- La amplitud
- El desfase
- La elongación
Respuestas: 1) 0,5 m; 2)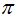 
radianes; 3) -0,5 m
Solución.
Si escribes una fórmula de la elongación, por ejemplo:
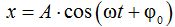y la comparas con la que nos han propuesto:
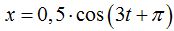vemos que A = 0,5 y el desfase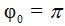 
Calculamos el valor de la elongación al comienzo del movimiento, es decir, cuando el tiempo es 0:
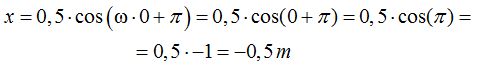
1.134 Si te dicen que un movimiento armónico está representado por la ecuación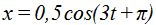 
y te preguntan cuántas variables tienes en ella ¿qué respondes?
Respuesta: Solo el tiempo t porque x está en función de t.
1.135 Un móvil se mueve con un movimiento armónico simple de A = 8 cm, siendo 4 cm el valor de la elongación en el momento en el que t = 0s y cuando t = 1s alcanza su máxima longitud, es decir, A.
Calcula: 1) El desfase y 2) La frecuencia.
Respuestas: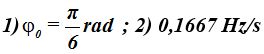 
Solución
Escribimos la fórmula de la elongación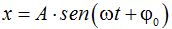 
1) Cuando t = 0 sabemos que x = 4.
Estos datos los sustituimos en la fórmula:
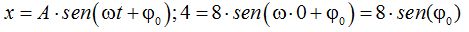
Hemos llegado a: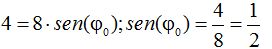 
El arco cuyo seno vale 0,5 sabemos que corresponde a 30º que pasando a radianes:
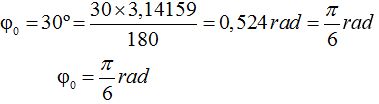
2) Vamos a averiguar la frecuencia.
Sabemos que la sencilla fórmula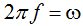 
contiene a la frecuencia pero para aplicarla necesitamos conocer el valor de la velocidad angular o pulsación.
No importa porque nos dicen que el valor de la elongación para cuando t = 1 equivale a 8 cm.
Volvemos a aplicar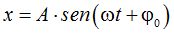 
y sustituimos los valores que conocemos:
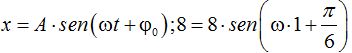
Dividimos ambos miembros por 8:
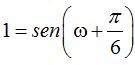
y vemos que el seno del ángulo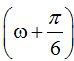 
vale 1. Sabemos que el seno de 90º vale 1 y que 90º es lo mismo que 
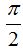radianes y haciendo las operaciones paso a paso llegamos a:
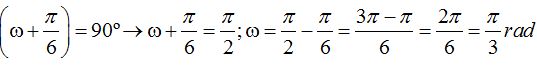
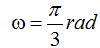
Conocida la velocidad angular la sustituimos en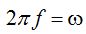 
y haciendo sustituciones y operaciones paso a paso llegamos a:
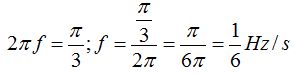
Recuerda que la frecuencia la damos en hercios por segundo.
1.136 Un móvil se mueve con un movimiento armónico de ecuación:
.
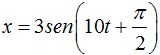Calcula la elongación en cm. cuando t = 3 s, la frecuencia angular y la fase inicial.
Respuestas:
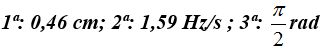
Solución.
La elongación en el segundo 3 vale:
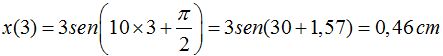
Necesitamos conocer la velocidad angular para hallar la frecuencia:
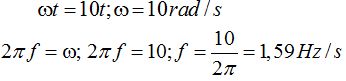
La fase inicial, por los datos del problema vemos que vale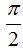 
rad.
