Movimiento rectilíneo uniformemente acelerado (M.R.U.A.)
1. La aceleración
Un cuerpo posee un movimiento acelerado cuando varía su velocidad.
La velocidad puede cambiar porque:
- Cambie su módulo. Se refleja en que su gráfica s-t es curva y, por tanto, su ecuación no es de primer grado. También, en que la gráfica v-t tiene pendiente, o lo que es igual, su valor cambia con el tiempo.
- Cambia su dirección. Cuando el móvil lleva una trayectoria curva, la velocidad (que es tangente a la trayectoria), cambia su dirección.
Una vez que se sabe que un movimiento es acelerado, se necesita una magnitud que indique cómo de acelerado está, una magnitud que permita comparar las aceleraciones de diferentes movimientos.
"La aceleración (a) es la variación de la velocidad en la unidad de tiempo. En el S.I. se mide en m/s2".
En los movimientos rectilíneos la aceleración se representa por un vector tangente a la trayectoria, en el sentido de la velocidad si aumenta su módulo y en sentido contrario si disminuye su módulo.
Nosotros estudiaremos dentro de los movimientos rectilíneos únicamente el caso en que la velocidad cambia de forma uniforme (constante).
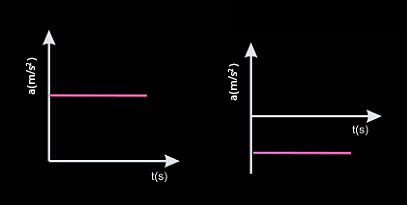
2. Movimiento rectilíneo uniformemente acelerado (M.R.U.A.)
Un movimiento es rectilíneo uniformemente acelerado cuando su trayectoria es una recta y el módulo de la velocidad cambia de forma constante.
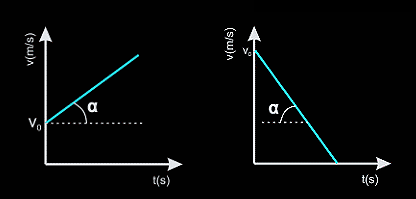
2.1 Relación v-t en un MRUA
La ecuación que relaciona la velocidad en función del tiempo es:
v=v0+a·t
Donde:
v= velocidad en cualquier instante
v0= velocidad inicial del móvil
a= aceleración
Cuando se realiza la representación gráfica, la pendiente de ésta es la aceleración. Si la velocidad aumenta, la aceleración tendrá el mismo signo que la velocidad, por lo que la pendiente de la gráfica será positiva. Si la velocidad disminuye, la aceleración tiene signo contrario a la velocidad, y por ello la pendiente será negativa.
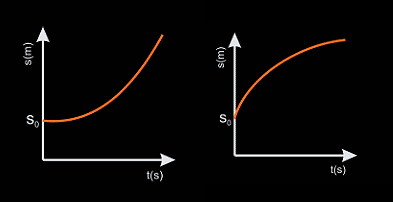
2.2 Relación s-t en un MRUA
La ecuación del movimiento es la siguiente:
Donde:
s=posición en cualquier instante
s0=posición en el instante t=0s
v0=velocidad inicial del móvil
a=aceleración
Cuando calculemos una magnitud (velocidad, aceleración, tiempo, etc.) con una ley de movimiento las unidades empleadas deben ser homogéneas. Es decir, si la aceleración viene expresada en m/s2 , no podremos poner la velocidad en km/h, ni el tiempo en otra unidad que no sean segundos.
Para evitar confundirnos pasaremos todas las magnitudes previamente a unidades del Sistema Internacional.
Tiempo en segundos
Velocidad en m/s
Espacio recorrido en metros
----0----
Ejercicio:
Un ciclista que circula a 18 km/h, mantienen una aceleración constante de 0'4 m/s2 durante 10 s. Calcular la velocidad que ha alcanzado al cabo de ese tiempo.
Solución:
Pasamos la velocidad inicial al S.I.
La velocidad final viene dada por:
----0----
Ejercicio:
Un motorista que lleva una velocidad de 60km/h acelera hasta alcanzar una velocidad de 100 km/h en 20s manteniendo una aceleración constante. Hallar el valor de la aceleración y el espacio recorrido.
Solución:
Las velocidades inicial y final en el S.I. son:
Por lo tanto la aceleración será:
El espacio recorrido será: