Movimiento rectilíneo uniforme (MRU)
1. Movimientorectilíneo uniforme (MRU)
La trayectoria de los movimientos rectilíneos es una recta, por tanto la dirección del vector velocidad, es siempre la misma.
Que el movimiento sea uniforme informa que el módulo de la velocidad no cambia.
"En un movimiento rectilíneo y uniforme, el vector velocidad no cambia de módulo ni de dirección; es constante."
2. Relación s-t (posición y tiempo) en un MRU
La gráfica s-t del movimiento uniforme es una recta, y su pendiente el módulo de la velocidad. Por ello la "ecuación del movimiento uniforme" toma la siguiente forma:
s = s0 +v·t
Que también podemos expresar como:
Donde:
s: posición en cualquier instante
s0: posición en el instante (t=0)
v: velocidad del móvil
t: tiempo
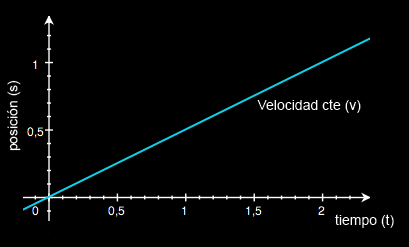
No se puede confundir la recta que nos sale al representar la ecuación del movimiento (s-t), con la trayectoria del movimiento. La misma gráfica s-t, sirve tanto si la trayectoria es rectilínea como curvilínea, lo que importa es que la velocidad es constante en todo el trayecto.
3. Relación v-t (velocidad y tiempo) en un MRU
El módulo de la velocidad no cambia con el tiempo. Si la velocidad es positiva, su representación quedará en la parte positiva de los valores del módulo de velocidad, y se situará por debajo cuando la velocidad tenga el sentido contrario.
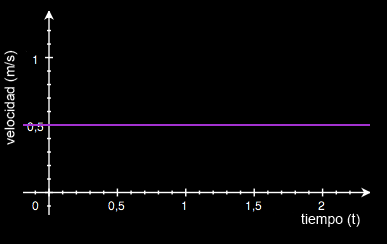
Recordemos que s-s0 es el desplazamiento. Además el desplazamiento coincide con el espacio recorrido, ya que la velocidad no cambia su módulo.
De la ecuación:
s = s0+v·t
Se deduce:
----0----
Ejercicio:
Un automóvil que circula con una velocidad constante de 90 km/h pasa por el poste indicador de 200 m en el momento en que se pone en marcha el cronómetro para medir el tiempo. ¿Cuál será su posición en el instante t=12 s?
Solución:
Pasamos primero la velocidad al S.I
Aplicamos la ecuación general de la posición para un m.r.u.
----0----
Ejercicio:
Calcular la velocidad que mantiene un peatón si pasa por la indicación de 40m en el instante t=0s y por la indicación de 80m en el instante t=25s.
Solución:
La ecuación general de la posición para un m.r.u. viene dada por:
s = s0+v·t
Donde según los datos s0=40 m. Si despejamos la velocidad y sustituimos los datos conocidos tendremos: