Movimiento circular uniforme (MCU)
1. Movimiento circular uniforme (MCU)
Cuando un móvil describe una circunferencia decimos que su trayectoria es circular.
La velocidad con la que la recorre puede ser constante o no.
En los movimientos circulares la velocidad recibe el nombre de velocidad angular, puesto que el móvil, mientras se desplaza por la circunferencia, va recorriendo ángulos.
En el MCU la dirección de la velocidad lineal cambia constantemente y la velocidad angular es constante.
La ecuación del movimiento circular uniforme es la siguiente:
Donde:
= ángulo recorrido en un tiempo expresado en radianes (SI)
= ángulo inicial expresado en radianes (SI)
w = velocidad angular (rad/s)
La velocidad angular, también se suele dar en otras unidades diferentes de las del SI como revoluciones por minuto (rpm) o vueltas por segundo (vueltas/s).
Para transformar estas unidades al SI se utilizan como siempre los factores de conversión.
1 vuelta = 1 revolución = radianes = 360º
2. Relaciones entre magnitudes lineales y angulares
Cuando un móvil recorre un arco, en realidad está recorriendo un espacio (e). Su trayectoria es la longitud de ese arco. Su relación con el arco es:
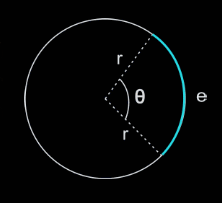
Donde r es el radio de la circunferencia.
La velocidad lineal es directamente proporcional a la velocidad angular, siendo la constante de proporcionalidad el radio de giro.
De la expresión anterior deducimos la relación entre la velocidad lineal (v) y la angular (w):
3. Periodo y frecuencia en el movimiento circular
3.1 Periodo (T)
El periodo (T) es el tiempo que tarda el móvil en pasar nuevamente por el mismo punto; o dicho de otra forma, el tiempo que tarda en dar una vuelta completa.
Se puede relacionar con la velocidad angular teniendo en cuenta que, al dar una vuelta completa =
radianes y el tiempo que se tarda en dar una vuelta, es el periodo (T). Por tanto, tendremos:
La unidad del periodo en el SI es el segundo.
3.2 Frecuencia (f)
La frecuencia (f) es el número de vueltas que realiza el móvil en cada segundo.
Esta magnitud se puede relacionar, igualmente con cierta facilidad, con el periodo y con la velocidad angular:
----0----
Ejercicio:
Determinar la velocidad angular y la velocidad lineal de la Luna en su movimiento orbital alrededor de la Tierra, sabiendo que tarda 28 días en cada vuelta y la distancia Tierra-Luna es de 384.000 km.
La velocidad angular será:
Y su velocidad lineal será: