Estructura Óptima de Capital

Ahora vamos a analizar si las decisiones sobre la estructura de capital crean valor al accionista, es decir, si existe una estructura óptima de capital que maximice el valor de mercado de la empresa.

Para responder a este planteamiento se puede acudir a la teoría del apalancamiento financiero.

La teoría del apalancamiento financiero se plantea apara responder una serie de cuestiones:

¿el ratio de endeudamiento tiene alguna influencia sobre la rentabilidad del accionista? ¿se puede cuantificar?
¿el nivel de deuda tiene alguna influencia sobre el riesgo asociado a la rentabilidad media del accionista? ¿se puede cuantificar? ¿se puede establecer alguna norma de actuación para satisfacer los objetivos del accionista?

La rentabilidad del accionista (r) es el cociente entre el beneficio neto (BN) y el volumen de fondos propios (FP):

R = BN / FP

El ratio de endeudamiento (L) es el cociente entre el volumen de fondos ajenos (FA) y el volumen de fondos propios (FP):

L = FA / FP

La rentabilidad del activo (R) es el cociente entre el beneficio antes de intereses e impuestos (BAIT) y el total de fondos de la empresa (FT):

R = BAIT / FT = BAIT / (FP+FA)

Se sabe que el beneficio neto es:

BN = BAIT – I – T

Y que los impuestos se pueden calcular de la siguiente forma:

T = BAT x t

Donde BAT es el beneficio antes de impuestos y t la tasa impositiva.

Por tanto:
BN = BAIT - I – BAT x t = BAIT – I – (BAIT – I) x t = (BAIT – I)x(1-t)

Dividiendo ambos miembros entre los fondos propios:
BN / FP = (BAIT – I)x(1-t) / FP
Operando se llega a:

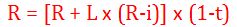
Esta es la ecuación fundamental del apalancamiento financiero, de donde se pueden extraer algunas conclusiones:

Si R>i, es decir, si la rentabilidad del activo supera al coste del pasivo ajeno, cuanto mayor sea L, mayor es r. En este caso, la rentabilidad del accionista aumenta conforme la empresa eleva su endeudamiento, es decir, a mayor ratio de endeudamiento, mayor rentabilidad obtenida por los accionistas: la deuda favorece la rentabilidad del accionista.
Si R<i, es decir, si la rentabilidad del activo es menor que el coste del pasivo ajeno, cuanto mayor sea L, menor es r. Conforme la empresa incrementa su nivel de endeudamiento, la rentabilidad del accionista disminuye, es decir, la deuda perjudica la rentabilidad del accionista.
Si R=i, entonces r = R x (1-t), sea cual sea L. En este caso, la rentabilidad del accionista no depende del ratio de endeudamiento, es decir, la deuda es indiferente para la rentabilidad del accionista.

Por otra parte, en un contexto de riesgo, hay que matizar lo anteriormente expuesto, porque, como se ha visto, cuanto más se endeude la empresa mayor será la rentabilidad esperada por el accionista, pero también será mayor el riesgo que soporta.

Por tanto, se derivan las siguientes conclusiones:

Si R>i, es decir, si la rentabilidad del activo es mayor que el coste de la financiación ajena, al accionista le interesa la deuda desde el punto de vista de su rentabilidad. Pero el incremento de deuda siempre aumenta esta rentabilidad.
Si R<i, es decir, si el coste del pasivo ajeno es mayor que la rentabilidad del activo, al accionista no le interesa la deuda ni desde el punto de vista de la rentabilidad ni del riesgo. En este caso, un aumento del endeudamiento provoca una menor rentabilidad del accionista, así como un incremento del riesgo de la misma.

Resumiendo, en ambiente de riesgo y siempre que la rentabilidad del activo sea mayor que el coste de la financiación ajena, el accionista verá aumentada su rentabilidad al aumentar su endeudamiento.

Pero debido a que el riesgo asociado a esta rentabilidad también incrementa, el accionista escogerá el ratio de endeudamiento más adecuado.

Ejemplo:

Una empresa tiene unos fondos propios por valor de 150.000 euros, unos fondos ajenos valorados en 180.000 euros con un coste antes de impuestos del 10% y una rentabilidad del activo, R = 15%. ¿Cuál será la rentabilidad del accionista sabiendo que la tasa impositiva es del 35%?

Solución:

L = CA / CP = 180.000 / 120.000 = 1,5
R = [R + L x (R-i)] x (1-t) = [0,15 + 1,5 x (0,15-0,10)] x (1-0,35) = 14,625%