Análisis de tendencias: Regresión
Regresión lineal
La regresión es una formulación matemática que permite identificar el grado de aproximación que tiene una recta con la que se intenta relacionar un conjunto de valores que se obtengan al medir dos variables en varios momentos. Los valores obtenidos en la observación se ubican en un gráfico de coordenadas produciendo lo que se denomina un gráfico de dispersión.
El método matemático para determinar la recta que se ajusta mejor a un conjunto de valores localizados en un gráfico de dispersión se llama “Ajuste de los Mínimos Cuadrados” y la forma más expedita de calcularla es en Microsoft Excel. Una explicación efectiva se encuentra en
https://www.youtube.com/watch?v=r7D2lgI2hQE
La fórmula de los mínimos cuadrados permite dibujar la recta que minimiza los cuadrados de los valores de las distancias de cada punto a la recta proporcionando los valores para a y b en la ecuación Y= ax + b y un coeficiente r² que indica en qué grado la recta se ajusta a los valores de la variable independiente.
La resultante es una recta como la dibujada en el gráfico siguiente. Y puede ser cualquier variable que aumenta o disminuye con el tiempo: precios, producción, alumnos, etc.
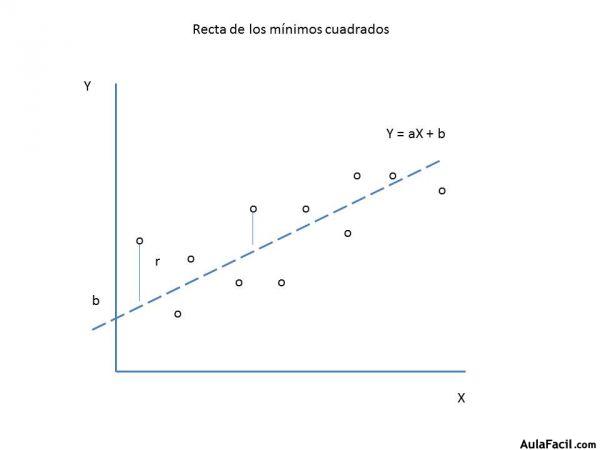
Como se ve en el gráfico, la recta resultante en este ejemplo se acerca bastante a los puntos que la originan. El valor del índice r² en este caso se aproximaría a 1 indicando que la recta es bastante acertada. La continuación de ésta hacia más adelante puede ser un predictor razonable de lo que se espera en el futuro.
Un desarrollo más extenso de este tema se encuentra en: