Regresión Simple (I)
Cuando dos variables se encuentran entrelazadas o relacionadas, y conocemos una de las dos variables, ésta nos brinda información sobre el resultado obtenido en la segunda variable. Así por ejemplo, el peso y altura de los niños; nivel de ingresos de un país y nivel de vida de su población; grado de criminalidad y fallecidos en un país, etc., y es aquí donde el Coeficiente de Correlación nos permitirá cuantificar dicha relación.
Al momento de establecer relaciones entre las variables, diferenciaremos aquellas variables que están relacionadas de forma exacta o funcional, y las que no lo están. Por ejemplo, el espacio recorrido por un automóvil está en “función” de la velocidad que llevaba y la duración de la misma. Este tipo de relaciones es la llamada relación funcional.
Pero resulta que éste tipo de relación “funcional” entre variables, que es muy común en áreas como la Física, no puede ser trasladada a otras ramas de la ciencia, como por ejemplo, las Ciencias Sociales. Por ejemplo, si conozco que una persona mide 1.75 c.m., calza zapatos 39 y es del sexo masculino, podría inferirse que ésta persona pesa entre 75 y 90 kilos, pero no hay exactitud en el hecho, sino meramente suposiciones.
En la regresión simple, el modelo general de estudio es el siguiente:
Yi = f (Xi) + ei
Donde:
Yi = variable dependiente
Xi = variable independiente
ei = representa la desviación o inexactitud de f(Xi) con respecto a Yi.
Si se fijan ustedes, en un modelo de Regresión Simple se posee una variable independiente y una variable dependiente. Para aclarar bien lo anterior, basémonos en un ejemplo con aplicaciones del SPSS.
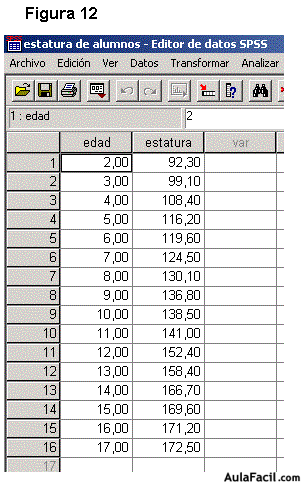
En la figura 12 se observa la base de datos que utilizaremos para realizar en análisis de regresión simple. Se tienen promedios de estatura de niños de 2 años hasta jóvenes de 17 años. Estos son promedios de estatura obtenidos en un colegio hipotético.
