Función exponencial

El caso de una ecuación exponencial requiere de un tratamiento especial, el crecimiento exponencial se le aplica en la mayoría de variables poblacionales.

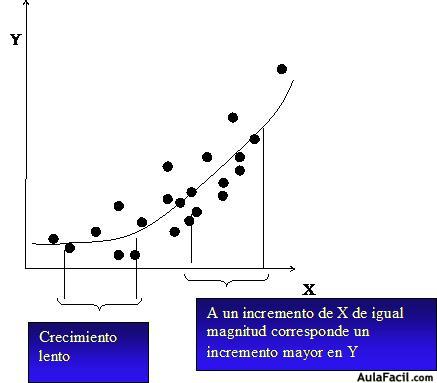
La explicación se debe entre otras, además de la relación gráfica, a que el crecimiento en un tramo es lento y a partir de cierto punto, este se incrementa en mayor cantidad, tal como muestra la siguiente gráfica.

La forma de la función estimada es

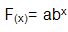
Los coeficientes “a” y “b” se calculan a partir de un sistema de ecuaciones que a continuación se explicara, el primer paso a realizar es linealizar la función para ello se aplican logaritmos base 10.

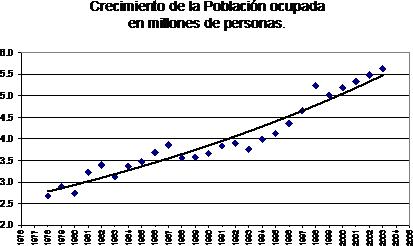
Teniendo el siguiente cuadro que relaciona tiempo y niveles Población ocupada, se puede observar una tendencia no lineal, una curvatura en la secuencia de datos, la forma gráfica muestra que el modelo de regresión mas adecuado es la exponencial.

Es necesario aclarar que cuando se relaciona el tiempo y otra variable, se considera al tiempo como la variable independiente.