Circunferencia tangente a dos rectas y a una circunferencia tangente a ellas

Circunferencia tangente a dos rectas y a una circunferencia tangente a ellas.

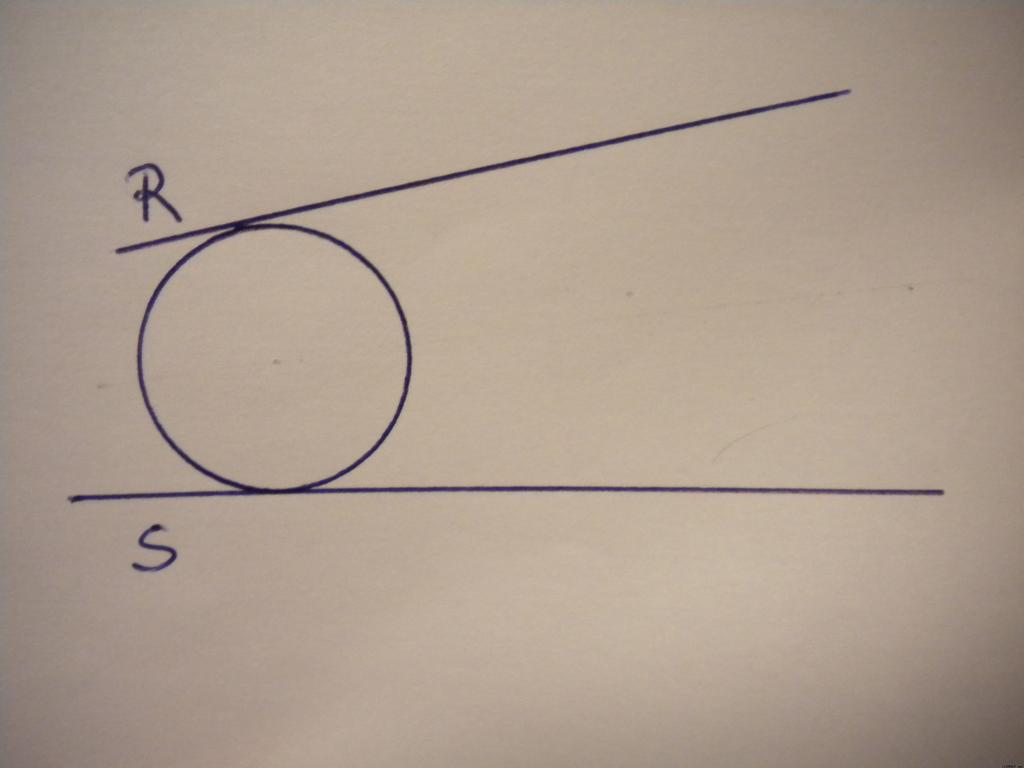
Como ya hemos señalado, el centro se encuentra en la bisectriz del ángulo que forman las rectas (segundo principio). Si consideramos que la tangente es perpendicular a la recta que une los centros, y que esta tangente también lo será de la circunferencia resultado, podemos reducir el problema a una circunferencia tangente a tres rectas.

• Como las rectas se cortan fuera del papel no podemos hacer la bisectriz de R y S, mediante paralelismo construimos dos nuevas rectas que se corten, R1 y S1.

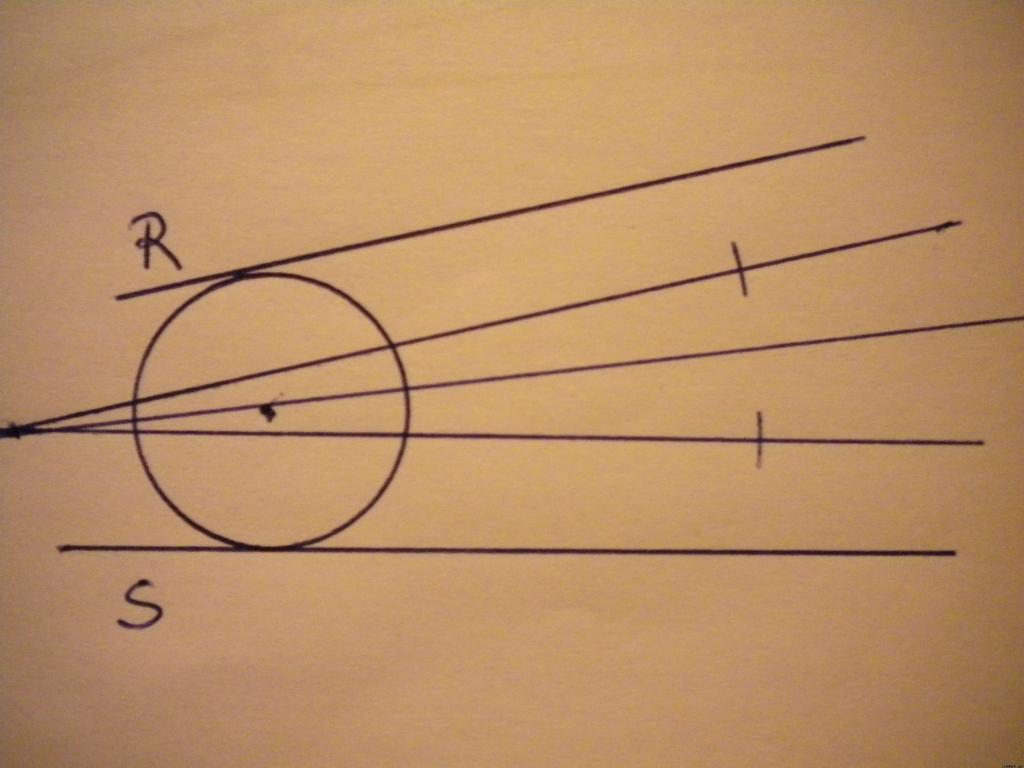
• Trazamos la bisectriz a R1 y S1. Donde corte la bisectriz con la circunferencia es un punto de tangencia. Por este punto trazamos una perpendicular.

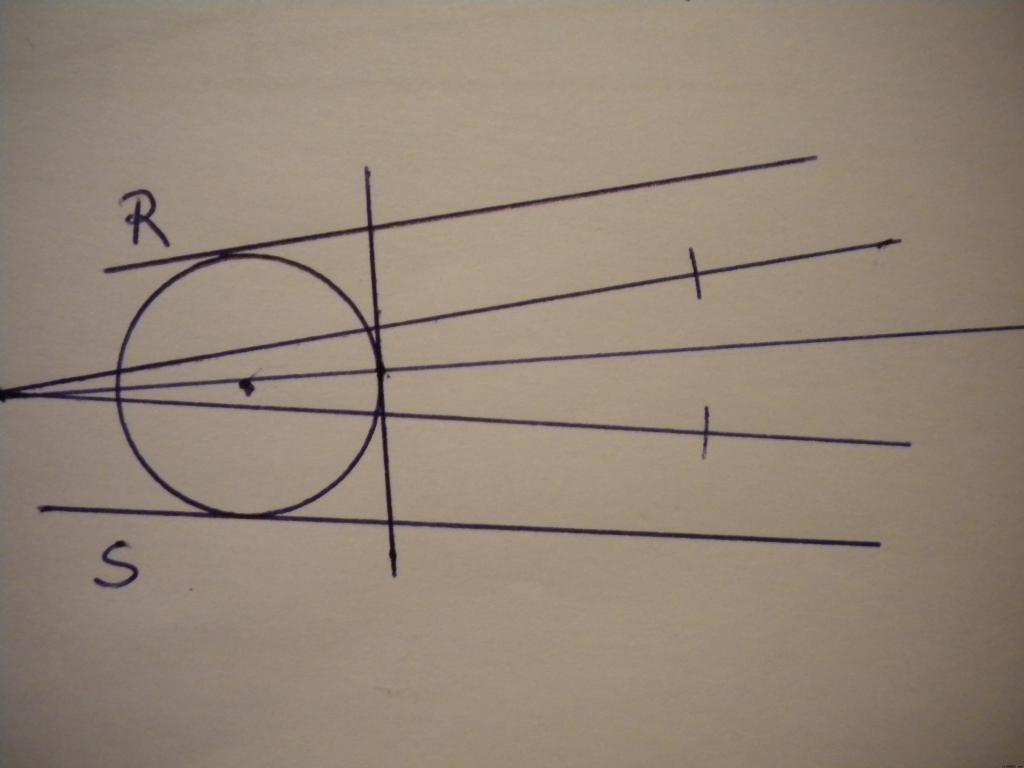
Después trazamos dos bisectrices, como vimos antes, para hallar la circunferencia tangente a tres rectas.