Sistema diédrico: sección y verdadera magnitud
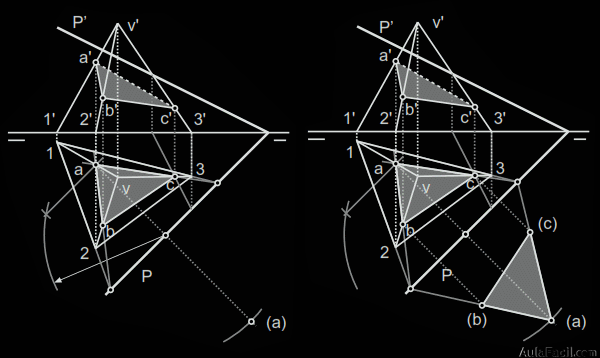
1. Trazado de la sección en verdadera magnitud de la pirámide de base triangular conociendo las trazas del plano seccionante P
Tenemos los datos de la proyección de la pirámide y las trazas del plano que la corta.
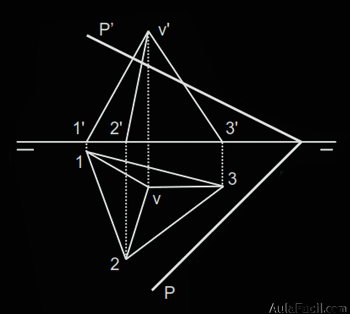
Para hallar la sección vamos a usar los conceptos de afinidad y homología que hemos aprendido en las lecciones anteriores.
Trazado:
1.) Procedemos a hallar la sección, para ello contendremos cada una de las aristas en un plano proyectante para determinar, de uno en uno, los puntos de intersección del plano con cada una de las aristas.
Primero hallamos la intersección C de la recta 3V con el plano P, usando un plano vertical proyectante auxiliar.
A partir de ahora resolveremos la sección por una relación homológica entre la sección producida por el plano y la base de la pirámide. Ambos son triángulos homológicos. El centro de homología es el vértice superior (las radiaciones son las aristas desde el vértice hasta la base). La recta límite es la traza horizontal del plano P, en ella convergen (en los puntos dobles) las rectas homólogas que contienen los lados homólogos de los triángulos.
2.) Prolongamos el lado 1-3 de la base (en proyección horizontal) hasta cortar a la traza P en un punto doble que unimos con c. En la prolongación de esa recta encontramos sobre la arista 1-v el punto a, 1-3 es homólogo de a-c.
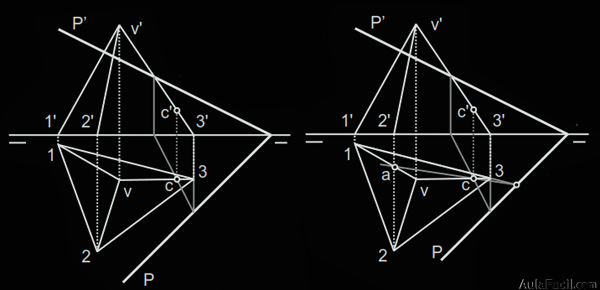
3.) Prolongamos el lado de la base 1-2 hasta cortar a P en el punto doble que unimos con a. La recta desde el punto doble hasta a corta a la arista de la pirámide 2-v en el punto b.
4.) Subimos la sección a la proyección vertical.
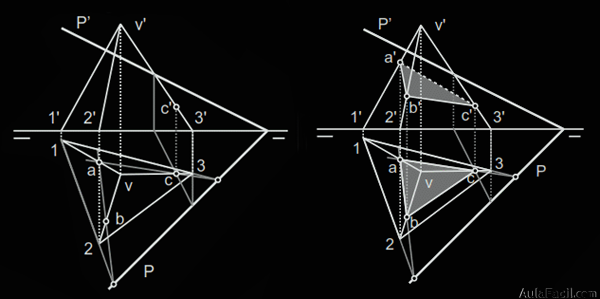
5.) Abatimos (sobre PH) el vértice a de la sección plana.
Trazamos una paralela al eje de afinidad (traza horizontal del plano o charnela) por la proyección horizontal del punto, sobre la paralela situamos la cota del punto.
La dirección de afinidad es perpendicular al eje de afinidad.
6.) Desde (a) trazamos una recta al punto doble sobre P de la recta ac. Desde c trazamos la dirección de afinidad que corta a la recta en(c), a-c es afín de (a)-(c).
Desde (a) trazamos una recta hasta el punto doble de a-b sobre P.
Desde b trazamos la dirección de afinidad para obtener (b) sobre la recta afín, a-b es afín de (a)-(b).
De este modo es mucho más sencillo, rápido y limpio resolver la sección plana en proyecciones y en verdadera magnitud del plano P con la pirámide.