Geometría métrica aplicada: proporcionalidad
1. Definición
Dos figuras son proporcionales si las relaciones de medidas entre las partes de una se corresponden con la relación de medidas de las partes de la otra.
También podemos entender la proporción como la relación existente entre las partes de una figura respecto a su totalidad.
2. Conceptos
2.1 Razón:
Es la relación que se establece entre las magnitudes de dos segmentos, a y b.
Se representa mediante una fracción: a/b, o como una división a:b.
Esta relación se puede establecer de dos maneras, obteniendo dos clases de razones :
- Razón aritmética: Relacionamos dos magnitudes y se compara cuánto excede una de la otra.
- Razón geométrica: Determinamos cuantas veces una magnitud contiene a la otra.
La razón constante de toda proporción geométrica se expresa mediante la letra k.
3. Proporcionalidad geométrica
Es la igualdad entre dos razones geométricas. Se representa por a/b = c/d, y se lee :
a es a b como c es a d.
Esta proporcionalidad puede ser de dos tipos :
- Proporcionalidad directa: Al aumentar un factor el otro aumenta en proporción y viceversa.
a1/b1 = a2/b2 = a3/b3 = ... an/bn = K - Proporcionalidad inversa: Al aumentar un factor el otro disminuye en proporción y viceversa.
a1/(1/b1) = a2/(1/b2) = a3/(1/b3 ) = ... an/(1/bn) = 1/K
4. Proporcionalidad de segmentos
La razón entre dos segmentos es el valor de la relación entre las magnitudes de ambos segmentos, siendo a, b, c y d los términos de la proporción.
Cuando relacionamos dos razones establecemos una proporción (proporción es la igualdad de dos razones: a/b= c/d).
- A los términos a y d se les denomina extremos.
- A los términos b y c se les denominan medios.
- A los términos a y b se les denominan antecedentes.
- A los términos c y d se les denominan consecuentes.
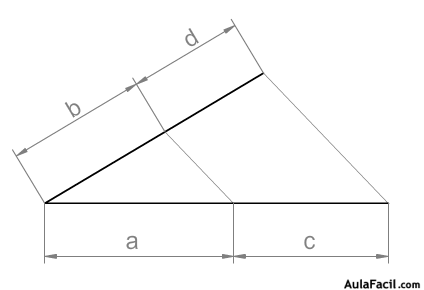
5. Tercera proporcional
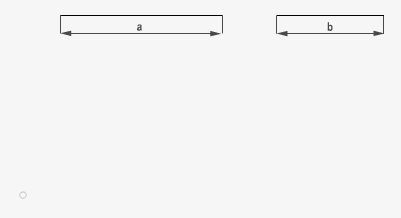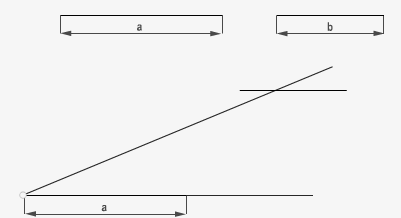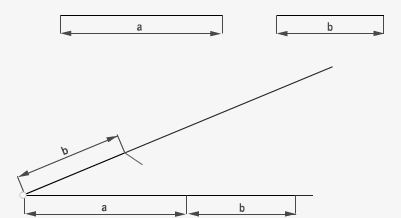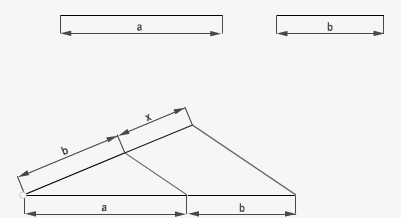
Cuando dos de los términos conocidos (extremos o medios) tienen el mismo valor cualquiera de los otros recibirá el nombre de tercera proporcional, a/b = b/x.
Dicho de otra forma es como una regla de tres donde dos de sus constantes son iguales, otra distinta y la cuarta sería la incógnita a resolver.
En este ejemplo hallamos la tercera proporcional (x), aplicando el teorema de Thales, de dos segmentos proporcionales que contienen a su vez dos segmentos del mismo valor (b).
6. Cuarta proporcional
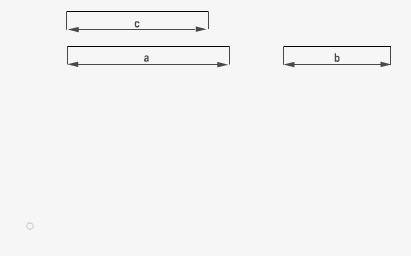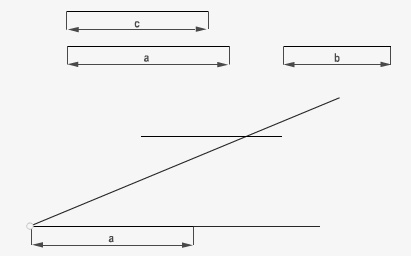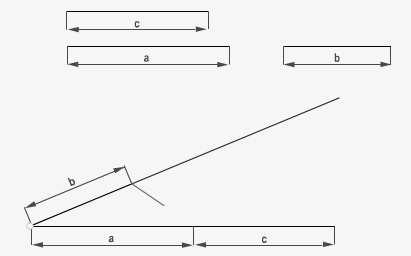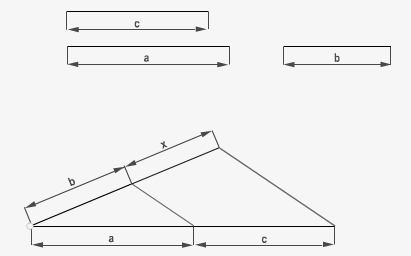
Cuando se conocen tres de los cuatro términos, se puede obtener el cuarto, éste recibe el nombre de cuarta proporcional. a/b = c/x. Dicho de otra forma lo podemos asimilar a una regla de tres normal, donde x es la incógnita a despejar. En este ejemplo volvemos a hallar x mediante el teorema de Thales pero en este caso los tres segmentos dados son distintos.
7. Media proporcional
La media proporcional o media geométrica es cuando cada uno de los términos medios o extremos de una proporción contínua son iguales.
Queda expresado de la siguiente forma:
siendo x la media proporcional.
Si despejamos x :
x·x=a·b
x2=a·b
Con lo que podemos decir también que para calcular la media proporcional de una proporción continua se extrae la raíz cuadrada del producto de los extremos.
7.1 Teorema de la altura: (suma de segmentos).
La media proporcional (x) de dos segmento a y b es la altura de un triángulo rectángulo, siendo su hipotenusa el segmento suma de los dos dados.
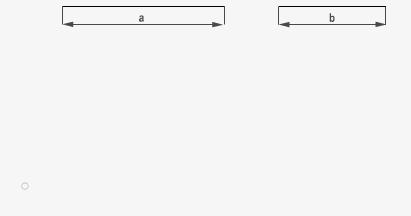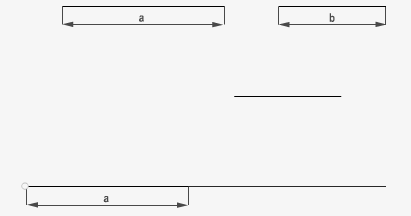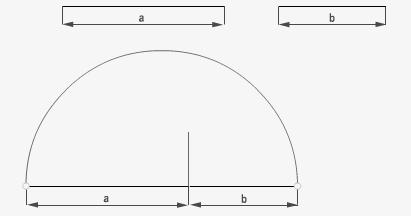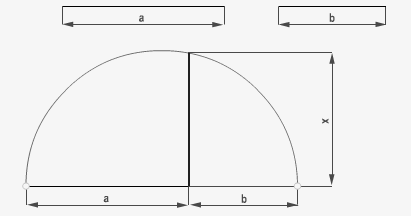
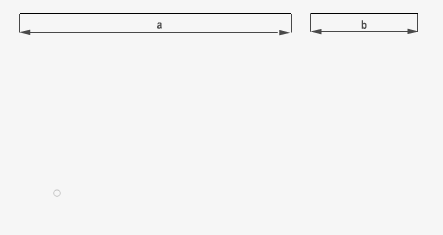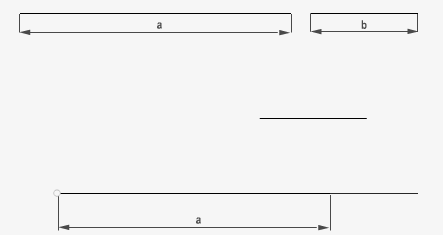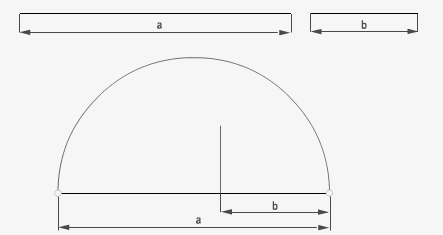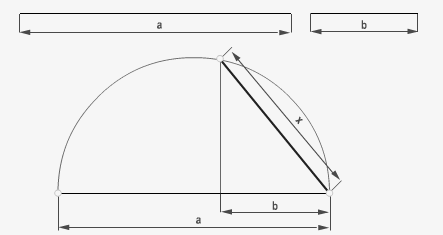
7.2 Teorema del cateto: (diferencia entre los segmentos).
La media proporcional es el cateto (mayor o menor) de un triángulo rectángulo, la proyección del dicho cateto sobre su hipotenusa (el segmento mayor dado) es igual a la longitud del segmento menor dado.