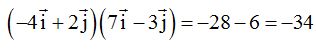Vectores unitarios en el plano. Coordenadas cartesianas de un vector respecto a la base canónica
Hemos estudiado los vectores 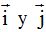 a los que llamamos unitarios porque sus módulos valen 1.
a los que llamamos unitarios porque sus módulos valen 1.
En la figura siguiente:
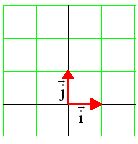
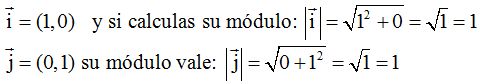
Vector unitario es el que su módulo vale 1.
Teniendo en cuenta la definición de vector unitario podemos decir que las coordenadas de un vector unitario pueden ser distintas a cero y a 1. Lo único que debes tener en cuenta es que su módulo valga 1.
Anteriormente estudiamos que para calcular el vector 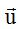 a partir de los vectores perpendiculares
a partir de los vectores perpendiculares 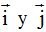 multiplicamos a sus módulos (de valor 1 cada uno) por los
multiplicamos a sus módulos (de valor 1 cada uno) por los
valores de las coordenadas de x y:
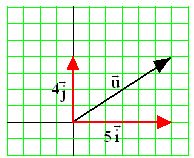
Es lógico que para hallar el vector unitario a partir de un vector cualquiera tengamos que dividir a sus coordenadas por su módulo.
Ejemplo:
En la figura anterior las coordenadas de 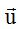 son (5,4).
son (5,4).
El módulo vale: 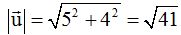
Si divido a las coordenadas (5,4) por 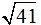 obtendré un nuevo vector cuyas
obtendré un nuevo vector cuyas
coordenadas serán el cociente de 5 y 4 entre 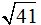 , es decir,
, es decir, 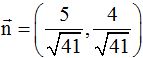
Comprobamos si el módulo del vector 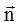 vale 1:
vale 1:
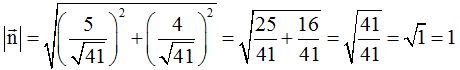
Efectivamente el vector 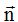 es unitario y tiene la misma dirección y sentido que el vector
es unitario y tiene la misma dirección y sentido que el vector 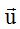 .
.
21.15 ¿Es unitario el vector 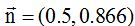 ? ¿Porqué?
? ¿Porqué?
Respuesta: Sí, porque su módulo vale 1
Solución
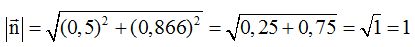
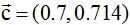 ? ¿ Porqué?
? ¿ Porqué?Respuesta: Sí, porque su módulo vale 1.
Solución:
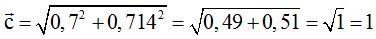
21.17 Las coordenadas del vector 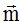 son (3,4)¿cuáles son las coordenadas de un vector unitario con la misma dirección y sentido que
son (3,4)¿cuáles son las coordenadas de un vector unitario con la misma dirección y sentido que 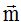 .
.
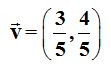
Solución
Para calcular las coordenadas de un vector unitario con la misma dirección y sentido al que nos proponen (recordamos lo que hemos dicho anteriormente), es la de dividir las coordenadas del vector dado entre el valor de su módulo:
Por ejemplo, las coordenadas del vector 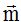 son(3,4)¿cuáles son las coordenadas de un vector unitario con la misma dirección y sentido que
son(3,4)¿cuáles son las coordenadas de un vector unitario con la misma dirección y sentido que 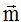 .
.
Calculo el módulo de 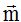 :
: 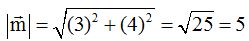 Ahora divido las coordenadas de
Ahora divido las coordenadas de 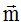 que son (3,4)entre el módulo que acabo de calcularlo que es 5.
que son (3,4)entre el módulo que acabo de calcularlo que es 5.
Las coordenadas del vector unitario con la misma dirección y sentido que 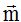 será (llamándole
será (llamándole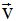 al vector unitario):
al vector unitario):
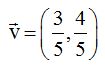
Lo comprobamos:
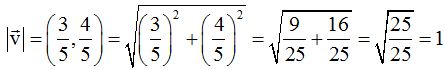
Vemos que el vector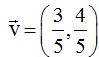 es unitario.
es unitario.
21.18 Supongamos el vector 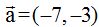 que lo referimos a la base canónica. Calcula un vector con la misma dirección y sentido que tiene
que lo referimos a la base canónica. Calcula un vector con la misma dirección y sentido que tiene 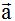 pero que sea unitario.
pero que sea unitario.
Respuesta:
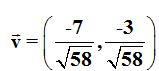
Solución
Después de calcular el módulo del vector 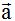 :
:
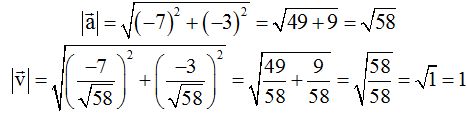
COORDENADAS CARTESIANAS DE UN VECTOR RESPECTO A LA BASE CANÓNICA
Las coordenadas cartesianas, es decir, con relación al eje de abscisas o eje y con relación al eje de las ordenadas o eje Y las expresamos (x,y).De este modo fijamos un punto en el eje de coordenadas.
Las coordenadas cartesianas de cualquier vector 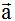 teniendo en cuenta los vectores unitarios podemos escribir:
teniendo en cuenta los vectores unitarios podemos escribir:
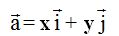
A x e y le podemos dar cualquier valor y de este modo obtendremos vectores diferentes:
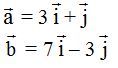
A partir de lo que acabas de estudiar realizamos el producto escalar de dos vectores en función de los vectores unitarios.
Es decir, calculamos del ejemplo anterior el producto de los dos vectores:
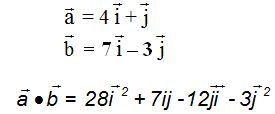
El producto 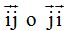 vale 0 porque si multiplicas las coordenadas de
vale 0 porque si multiplicas las coordenadas de 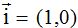
por las de 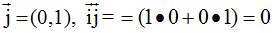
De momento, el producto vale: 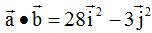 porque
porque 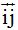 y
y 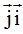 valen cero.
valen cero.
Como 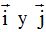 valen 1 cada uno de ellos,
valen 1 cada uno de ellos, 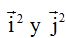 serán iguales a 1.
serán iguales a 1.
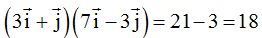
21.19 ¿Cuánto vale el producto: 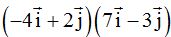 ?
?
Respuesta: -34 Solución: