Representación Gráfica de las Ecuaciones de Segundo Grado
Recordarás que cuando nos referimos a las ecuaciones de primer grado las representábamos por medio de una recta:
Ejemplo:
Tienes la ecuación 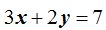 si das un valor a x obtienes otro para y, este valor lo llevábamos al eje de coordenadas y fijábamos un punto.
si das un valor a x obtienes otro para y, este valor lo llevábamos al eje de coordenadas y fijábamos un punto.
Dábamos otro valor a x y obteníamos el correspondiente a y .Con estos dos valores conseguíamos el segundo punto.
Al unir los dos puntos determinábamos la recta. Todos los puntos de la recta son respuestas de la ecuación.
En el caso de las ecuaciones de 2º grado su representación gráfica es muy diferente.
Supongamos una ecuación de 2º grado (el exponente de x debe ser 2): 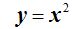
Vamos a dar valores a la variable independiente x y conseguiremos que la variable dependiente y tome los suyos:
En primer lugar damos a x el valor 3, luego 2, después 0, seguidamente – 2 y por fin, – 3. La variable dependiente y recibirá los valores: 9,4,0, 4 y 9
Podemos escribir:
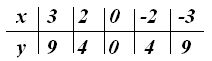
Colocamos en el eje de coordenadas los puntos:
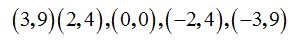
y luego, unimos esos puntos tal como lo ves en la figura siguiente:
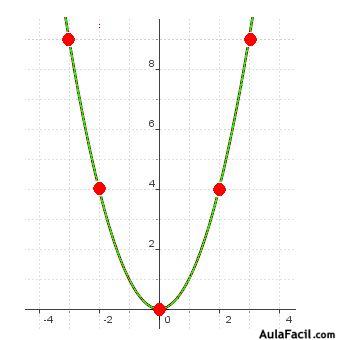
13.82 Representa gráficamente la ecuación de 2º grado: 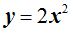
Respuesta:
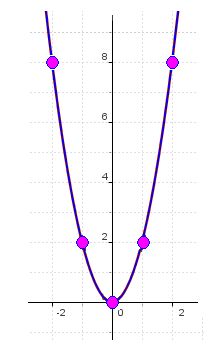
Solución
Dando valores a x : 2, 1, 0, -1 y -2 obtenemos los de y en la ecuación de 2º grado: 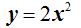
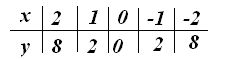
Fijados los puntos, los unimos y obtendremos la parábola.
¿Por qué los puntos no los unimos con rectas?
Porque si en la ecuación de 2º grado 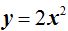 diéramos a x los valores que indicamos a continuación los correspondientes al eje y serían::
diéramos a x los valores que indicamos a continuación los correspondientes al eje y serían::
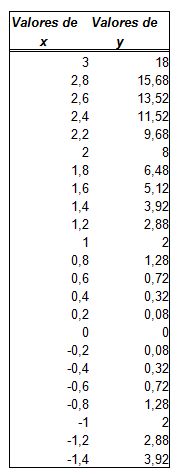
Estos valores obtenidos los llevamos al eje de coordenadas para crear los puntos y obtendríamos algo parecido a:
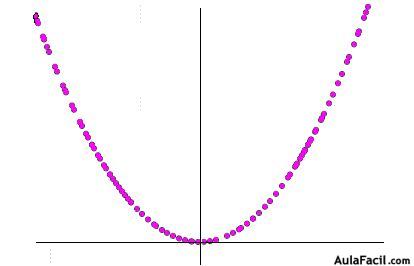
Por la colocación de los puntos, sin necesidad de unirlos puedes ver el resultado.
Vértice de la parábola
Si te has fijado bien, en todas las figuras referidas a la parábola has visto, por un lado, el eje de coordenadas y por otro, la parábola.
Llamamos vértice de la parábola al punto común de la parábola con el eje vertical de la misma o su eje de simetría.
No se trata del eje vertical o de ordenadas de un eje de coordenadas.
Nos referimos al eje de la parábola.
El eje de la parábola es un eje de simetría que divide a la parábola en dos curvas iguales. Cada una de estas curvas se llaman ramas o brazos de la parábola.
¿Qué es un eje de simetría en una parábola?
Es una línea de modo que si doblásemos el papel por dicha línea, las ramas de la parábola coincidirían.
Todas las figuras que has visto hasta ahora, el vértice lo tienen en el punto (0.0).
En todos los casos que vamos estudiando, el eje de la parábola coincide con el eje coordenadas, pero esto no es siempre así como veremos más adelante.
Vamos a dibujar una parábola cuyo vértice se encuentre en el punto (0,1).
En primer lugar debemos conocer la ecuación de 2º grado, supongamos que se trata de:
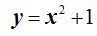
El vértice se hallará en el punto (0,1). Veamos porqué.
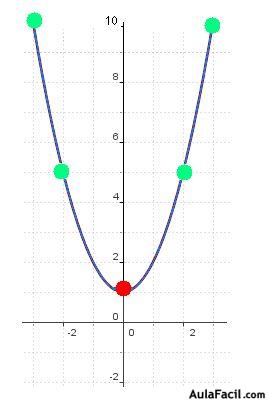
Si a "x" le das el valor cero en esta ecuación, comprobarás que el valor de y es 1. Luego, para x=0; y=1.
Fijamos este punto (color rojo) en el eje de coordenadas.
El resto de los puntos (en color verde), y obtenemos la parábola:
En el caso de que representásemos gráficamente la ecuación: 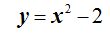
Para x=0 y=-2 La parábola sería:
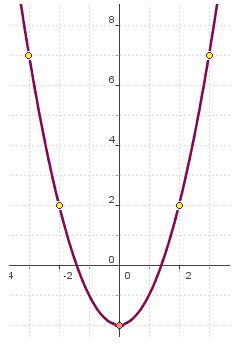
En el caso de que la ecuación fuese 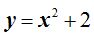 el vértice estaría situado en el punto (0,2):
el vértice estaría situado en el punto (0,2):
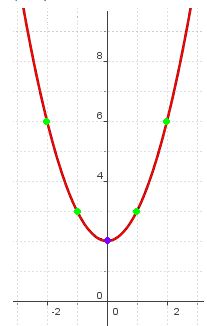
Si a x le das el valor 0 en la ecuación propuesta, y valdrá 2.
13.82(a) Representa gráficamente la ecuación: 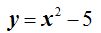
13.83 Representa gráficamente la ecuación: 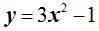
Respuesta:
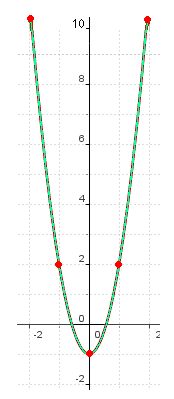
Solución
Los puntos que hemos tomado han sido:

El vértice de la parábola lo tenemos en el punto (0,-1)
¿Qué sucede con las coordenadas del vértice en el caso de la representación gráfica de una ecuación de 2º grado del tipo 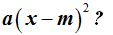
Cuando la ecuación de 2º grado es del tipo 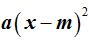 el vértice se traslada hacia la derecha tantas unidades como vale m.
el vértice se traslada hacia la derecha tantas unidades como vale m.
En el caso de 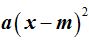 se traslada hacia la izquierda tantas unidades como vale m.
se traslada hacia la izquierda tantas unidades como vale m.
Ejemplo: 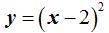
En este caso a vale 1.

Llevamos algunos de estos valores sobre el eje de coordenadas
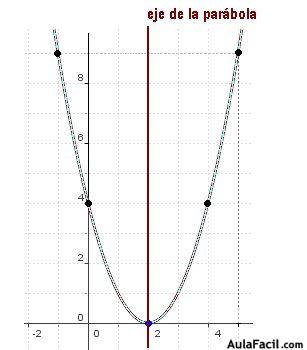
Cuando x = 2; el valor de y = 0. Este es el punto común de la parábola y su eje.
Si doblásemos el papel por el eje de la parábola, las dos ramas o brazos coincidirían.

13.84 ¿Cuáles son las coordenadas del vértice de la parábola correspondiente a la ecuación 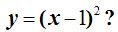
Respuesta: el punto (1,0)
13.85 ¿Cuáles son las coordenadas del vértice de la parábola correspondiente a la ecuación 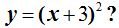
Respuesta: el punto (-3,0)
13.86 ¿Cuáles son las coordenadas del vértice de la parábola correspondiente a la ecuación 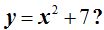
Respuesta: el punto (0,7)
13.87 ¿Cuáles son las coordenadas del vértice de la parábola correspondiente a la ecuación 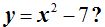
Respuesta: el punto (0,-7)

