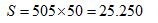Suma de los Términos de una Progresión Geométrica
Observa con atención lo que sucede con la suma de los términos de una progresión aritmética:
Supongamos la progresión:
2. 5. 8. 11. 14. 17. 20. 23. 26. 29. 32. 35. 38
Sumamos todos los términos y veo que S (la suma de todos los términos) vale 260
(1) S = 2+ 5+8+11+14+17+20+23+26+29+32+35+38= 260
Si sumo el valor de dichos términos comenzando por el último, la suma será la misma:
(2) S= 38+35+32+29+26+23+20+17+14+11+8+5+2+= 260
Ahora sumas las igualdades de las notas (1) y (2). La suma la haces verticalmente y te encontrarás con (2+38), (5+35), (8+32).......
Estás sumando el primer término con el último, el segundo con el penúltimo, el tercero con el antepenúltimo, y así, sucesivamente como tienes a continuación,verás que todas las sumas son iguales:
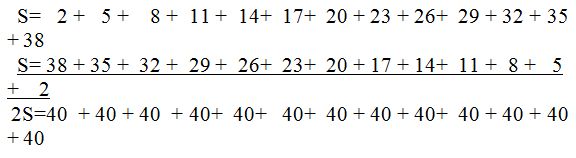
Hemos sumado los términos a la izquierda y la derecha del signo ‘=’ por ello: 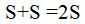
¿Cuántas veces se repite la misma suma? Si cuentas bien verás que 40 se repite 13 veces lo que equivale a 40 x 13= 520
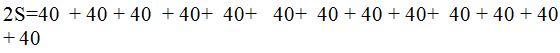
puedes escribir:
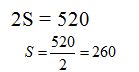
Si a los términos los escribimos como:

Los puntos suspensivos se refieren a otros términos, dependiendo del número de éstos.
Siendo n el número de términos 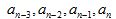 serán los cuatro últimos términos. En una progresión de 7 términos tendrás, sustituyendo n por 7:
serán los cuatro últimos términos. En una progresión de 7 términos tendrás, sustituyendo n por 7:
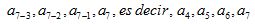
La suma de todos los términos será: 
El valor de la suma no varía si los sumamos comenzando del último al primero:
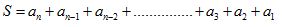
Ahora sumamos ambas igualdades:
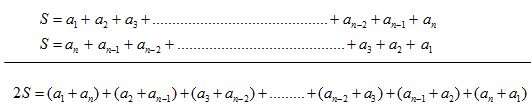
Todas las sumas indicadas entre paréntesis tienen el mismo valor por lo que podríamos escribir:

Como todos los sumandos entre paréntesis valen lo mismo, tomamos uno de ellos, los que se refieren al primero y último términos y nos resulta lo que tienes más arriba...
En lugar de sumar: 23+23+23+23+23+23, es más fácil, contar cuantas veces se repite este número y multiplicarlo por 23: 23+23+23+23+23+23 es lo mismo que 23x6.
¿Cuántas veces se nos repite 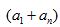 ?
?
Tantas veces como términos tenga la progresión, en este caso, n. Por lo que se nos transformaría todo lo anterior en:
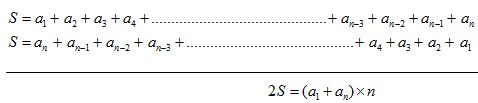
Despejamos el valor de S y obtenemos:
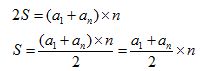
La fórmula que nos sirve para calcular el valor de la suma de los términos de una progresión aritmética es igual:
A la suma del primero y último términos, dividido por 2 y multiplicado por el número de términos.
Si una progresión aritmética tiene un número impar de términos, como:
2. 4. 6. 8. 10. 12. 14. 16. 18
La suma del primero y último, es igual a la suma del segundo y penúltimo,…. y me quedará el término CENTRAL sólo. Si a éste le multiplico por 2, es decir, hallo el doble de su valor, veré que coincide con las sumas anteriores:
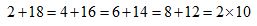
16. 15 Calcula la suma de los 20 primeros términos de la progresión 2. 4. 6. 8. ……….
Respuesta: 420
Solución:
Primero calculamos el valor del último término:
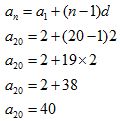
Aplicando la fórmula de la suma de los términos de una progresión aritmética:
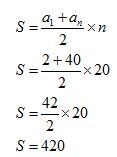
16.16 En una progresión aritmética el primer término vale 1, el segundo 3. …….La suma de todos los términos 196. ¿Cuántos términos tiene?
Respuesta: 14
Solución:
Conocemos el valor de 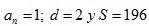
Aplicando la fórmula de la suma y haciendo operaciones:
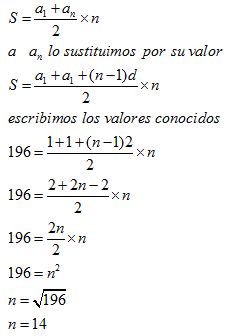
16.17 Calcula la suma de los 1000 primeros números naturales.
Respuesta: 500.500
Solución:
Conocemos el primer término que es 1. Conocemos el último que es 1000 y además sabemos que la d es igual a 1.
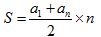
Haciendo uso de la fórmula de suma:
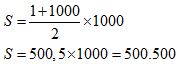
16.18 Calcula la suma de los 1000 primeros números impares.
Respuesta:1.000.000
Solución:
Conocemos el primer término, 1. La diferencia o razón, 2. El número de términos, 1000.
Calculamos el valor del último término:
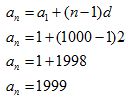
Aplicando la fórmula 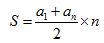 de la suma:
de la suma:
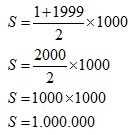
16.19 Calcula la suma de los 1000 primeros números pares.
Respuesta: 1.001.000
16.20 Calcula y demuestra que la suma de los 1000 primeros números pares más los 1000 primeros números impares es igual 2.001.000.
Respuesta: 2.001.000
Solución:
La suma de los 1000 primeros números pares hemos visto que vale: 1.001.000
La suma de los 1000 primeros números impares hemos visto que vale: 1.000.000 Total…………..: 2.001.000
Calculamos la suma de los 2.000 primeros números YA QUE EN ESTE NÚMERO ESTÁN INCLUIDOS 1.000 NÚMEROS PARES Y 1.000 NÚMEROS IMPARES:
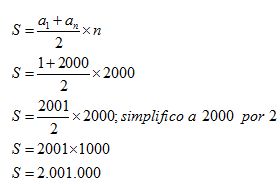
Veo que coinciden las dos cantidades lo que me indica que la respuesta es correcta.
16.21 Tenemos la progresión aritmética siguiente: 5,………………….995. 1000. Halla la suma de todos los términos.
Respuesta: 100.500
16.22 Calcula la suma de los 100 primeros múltiplos de 5.
Respuesta: 25.250
Solución:
El primero vale……. ……5
El último ……. ………….500
El número de términos….. 100
La suma 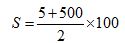 valdrá:
valdrá: