Factores unitarios o factores de conversión de unidades.
El método del factor unitario para resolver problemas en química se basa en ciertos puntos:
- Un factor es un número o fracción que multiplica a otro.
- Es una relación o división.
- Se le llama factor unitario debido a que tanto el numerador como el denominador equivalen a lo mismo. Por ejemplo, tenemos que 1 centena contiene 100 unidades.

Como se puede apreciar, una centena es lo mismo que 100 unidades.
- Para poder eliminar las unidades, debemos saber colocar bien los datos de acuerdo al principio matemático de eliminación. Si está en el numerador la unidad que deseamos eliminar, colocamos en el denominador la equivalencia: Por ejemplo, queremos obtener cuántas unidades hay en 3.4 centenas.

Siendo posible esto partiendo de que 3.4 centenas puede ser representado como fracción añadiéndole un 1 al denominador. Cuando ya tenemos establecidos nuestros factores, procedemos a multiplicar todos los numeradores y el resultado dividirlo entre el resultado de la multiplicación de todos los denominadores, o lo que es lo mismo, proceder de la forma en que se multiplican fracciones, es decir, de manera directa.

Ahora vamos a analizar un ejemplo práctico.
EJEMPLOS.
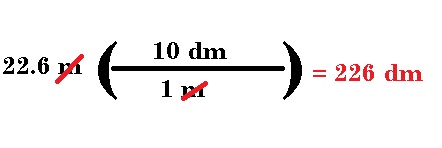
1.- Convierta 22.6 metros a decímetros.
Primero recordemos que un metro tiene 100 centímetros y un decímetro tiene 10 centímetros. Por lo cual podemos decir que en un metro hay 10 decímetros.
1 m = 10 dm
NOTA: No siempre se podrá analizar de esta forma las equivalencias, sino que la mayoría del tiempo se tendrán que obtener de alguna tabla de equivalencias o por memorización. Generalmente en los problemas se dan las equivalencias necesarias para la resolución.
Entonces después de eso, creamos nuestro factor y resolvemos. Como queremos eliminar los metros colocamos 1 metro en el denominador y en el 10 dm en el numerador:
2.- En una ciudad con demasiado tráfico, como la ciudad de México, se estima que unas 9.5 toneladas de plomo de los gases de escape se depositan cada día en las autopistas o cerca de ellas. ¿Cuál es la cantidad anual en kilogramos (1 ton = 2000 lb exactas; 1 lb = 0.454 kg; 1 mes 31 días; 1 año 12 meses)?
Para poder resolver este problema, tenemos que pasar por todas esas conversiones. Lo primero que tenemos que hacer es encontrar qué vamos a convertir. En este caso, queremos saber cuántos kilogramos de Pb vamos a generar en un año, partiendo de que se producen 9.5 toneladas por día, eso quiere decir que tenemos que colocar en el denominador 1 día.
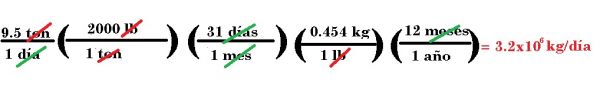
ACTIVIDAD. Resolver los siguientes problemas.
a) Convertir
25.4 m a kilómetros
|
|
242 lb a miligramos
|
|
68.3 cm3 a m3
|
|
b) ¿Cuántos segundos hay en un año solar (365.24 días)?
|
c) Un corredor al trote recorre dos millas en 15 minutos. Calcule la velocidad en:
(1 milla = 1609 m; 1 pulgada = 2.54 cm)
Pulgada/ segundo |
|
Metro/ minuto |
|
Kilómetro/ hora |
|