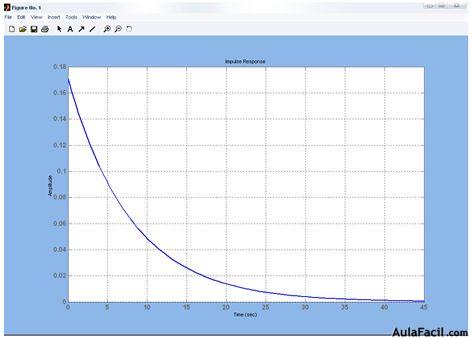
Diagrama de Bode y Gráfico de Respuesta Transitoria en MATLAB
Gm=e-s
Gv= 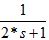
Gp=1.36/(7.97*s+1) Obtenido del proceso BM
Haciendo el programa en Matlab 2007 (7.4) obtenemos los siguientes resultados:
>> s=tf ('s')
Transfer function:
>> Gp=1.36/ (7.97*s+1)
Transfer function:
1.36
-----------
7.97 s + 1
>> Gv=1/ (2*s+1)
Transfer function:
1
-------
2 s + 1
>> G1=tf (1,'iodelay', 1)
Transfer function:
exp(-1*s) * (1)
>> Gm=pade(G1,1)
Transfer function:
-s + 2
------
s + 2
>> Sys=Gp*Gv*Gm
Transfer function:
-1.36 s + 2.72
-----------------------------------
15.94 s^3 + 41.85 s^2 + 20.94 s + 2
>> bode(sys1)
A continuación Matlab gráfica :
GRÁFICO Nº1
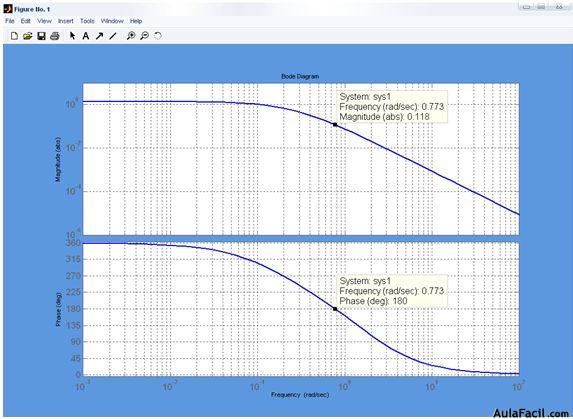
Entonces el sistema es estable. Ya que del gráfico se puede apreciar el valor de
w=0.776 Rad./seg.
AR=0.117
A continuación se analiza la respuesta transitoria a una variación de tipo paso e impulso según:
- Step: En matlab se escribe el siguiente comando, obteniéndose el gráfico Nº2:
>> step(Gp),grid;
GRÁFICO Nº2
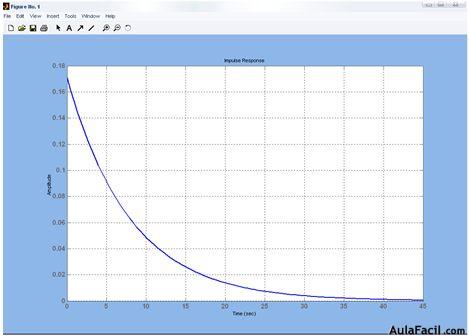
Se obtiene una amplitud de 0.859 para el t = τ=7.97s
- Impulso: Esta vez se tipea lo siguiente:
>> impulse(Gp),gris
GRÁFICO Nº3