Grafos Pert

Problema 19.

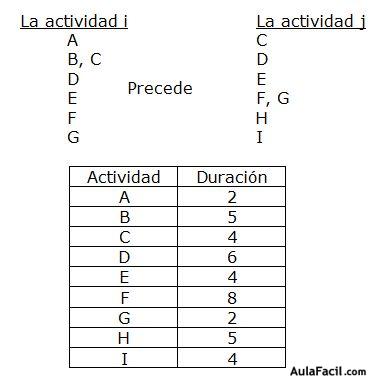
Construir el grafo PERT y determinar el camino crítico y la duración del proyecto cuyas actividades, duraciones e interrelaciones se expresan a continuación:

Solución

Para hacer este ejercicio hemos de dibujar un gráfico muy sencillo.

Comenzamos haciendo el primero de los nudos. Tiene esta forma.

Para dibujar el gráfico hay que seguir lo que dicen las tablas del enunciado, que se puede resumir en la tabla de precedencias, cuyo significado también se detalla:

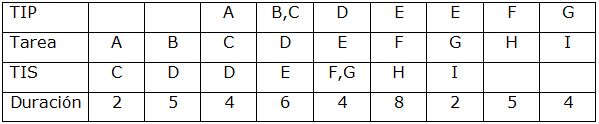
TIP: tarea inmediatamente precedente
TIS: tarea inmediatamente siguiente.

Cada vez que una flecha toca un punto, ahí debe de haber un nudo nuevo.

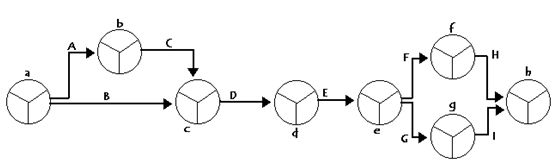
A continuación asignamos a cada nodo unas letras minúsculas, para diferenciarlas de las actividades (son las letras pequeñas que ya están puestas en la figura de encima). Esto ayudará a rellenar los primeros huecos de los nudos. Se trata del número de orden.
Los obtenemos según esta regla:

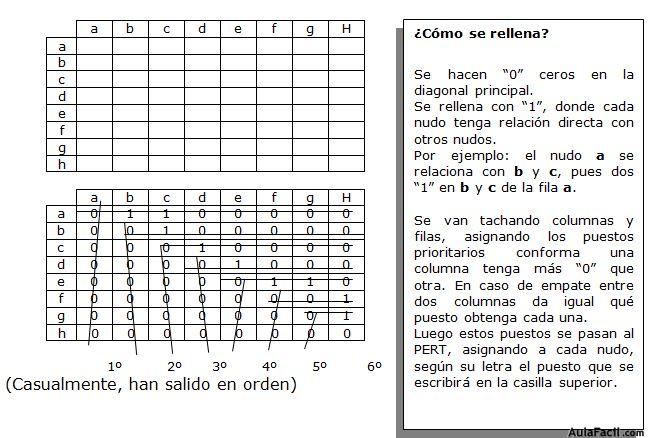
Con esa información numeramos los nudos llegando al siguiente gráfico:

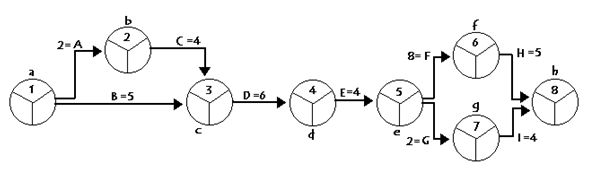
Para hacer el problema de forma más cómoda suele anotarse al lado de cada actividad su duración. Una vez anotado el número, quedan dos huecos en el nodo que servirán: la parte izquierda para el llamado tiempo early de cada nudo, y la parte derecha para el tiempo last. Hay que rellenarlos según otra regla. Primero se calculan todos los tiempos early (de delante hacia atrás) y se rellenan los correspondientes nudos. A continuación se calculan los tiempos last (de atrás hacia delante).

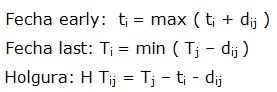
El primer nudo, el tiempo early siempre es 0. Mirando las precedencias de nuevo decimos: ¿de qué nudo vamos a calcular el tiempo EARLY?

Por seguir un orden, lo calculamos del nudo b. ¿Quién llega al nudo b? La actividad A. Por tanto la operación es è tiempo early del nudo desde el que viene A más la duración de A. Es decir, el tiempo early del nudo b, va a ser 2.

Siguiente nudo del que vamos a hallar el tiempo early: el nudo c. ¿quién llega al nudo c? Pues dos actividades, B y C. Como tenemos ahora dos flechas habrá que optar por una de las dos. ¿Cómo lo hacemos? Siguiendo un criterio. ¿Cuál de los tiempos early de los nudos de los que vienen estas dos flechas, es mayor? La de la actividad C. Pues el tiempo earlydel nudo que estamos operando será è tiempo early del nudo b más la duración de la actividad C. Es decir, 6.

Y así se hace para rellenar los tiempos early de cada nudo. Al acabar con éstos, el grafo resultante será:

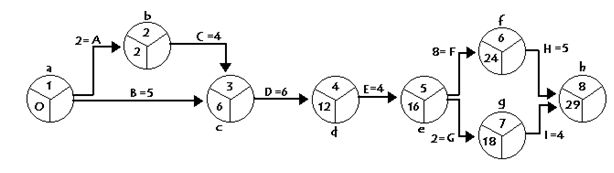
Los tiempos last se rellenan trabajando con el grafo de atrás hacia delante. Es decir, empezamos desde el último nudo. En él, su valor lastes igual a su valor early. Así que podemos copiarlo al lado.

Ahora nos preguntamos: ¿de qué nudo queremos hallar el tiempolast? Del nudo f. Para ello se toma el tiempolast del nudo que le precede y le restamos el valor de la duración de la flecha que enlaza esos dos nudos:

es decir, 29 –5 = 24, que es lo que ponemos en el hueco last del nudo f.

En el nudo g hacemos lo mismo. De forma que tenemos 29 – 4 = 25.

Para el tiempolast del nudo e, nos preguntamos: ¿ si ahora hay dos actividades que salen del nudo e, cuál cojo? Pues la que tenga el tiempo last menor, y a ese tiempo last se le resta el valor de la flecha que enlaza esos dos nudos, es decir, 24 – 8 = 16.

Así se hace sucesivamente hasta llegar al primer nudo, con lo que habrá quedado el siguiente grafo:

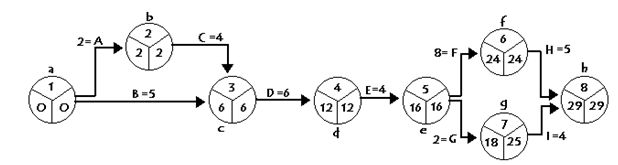
De esta manera ya puede conocerse que el tiempo que tarda la operación en llevarse a cabo es el equivalente en unidades temporales, al tiempo early o last del último nudo: o sea, 29 unidades de tiempo.

Hemos hallado el tiempo que dura la operación y hemos construido el grafo PERT, pero aún falta determinar el camino crítico. Se hace de la siguiente forma. Hallamos las holguras, que se averiguan restando los tiempos last a los tiempos early (por nudo).

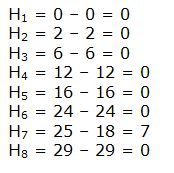
Y luego las holguras de las actividades, que se hacen Tiempo last – Tiempo early – Duración

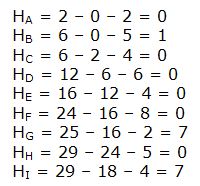
Hacemos el Camino Crítico con las actividades cuya holgura es igual a 0:

Acabados todos los caminos por precedencia, el grafo tiene que haber quedado de esta manera:

• En primer lugar vamos a atender a la lista de las precedencias. Dibujamos un nudo, (como el de la figura) y hacemos que de él salgan dos flechas, (por ser el primer nudo llevará dos flechas, y no una como el resto de nudos). Estas flechan las nombramos con las dos primeras actividades, (A y B).
• La flecha A, según el listado de precedencias, debe desembocar en la actividad C, porque la precede.
• De este nudo que ha formado la flecha A, sale la flecha C que junto a la flecha B han de apuntar hacia la actividad D, en un nuevo nudo. (Todo esto lo hacemos mirando las precedencias).
• De este último nudo surge una flecha, la D que acaba en un nudo que pertenece a la flecha E.
• La flecha E precede a F y G, por lo que del nudo que toque, saldrán dos flechas, precisamente F y G.
• Cada una de estas, (F y G) forma un nuevo nudo, del que parten respectivamente, las flechas de las actividades H e I, que apuntan hacia el último nudo del gráfico PERT.