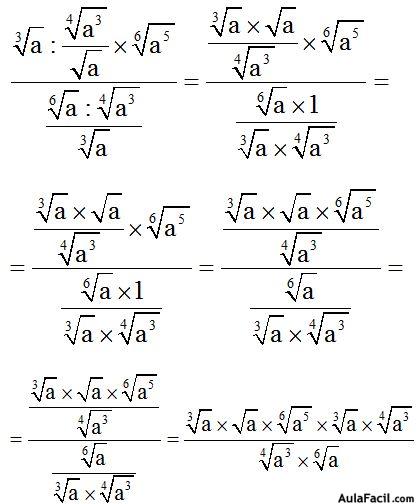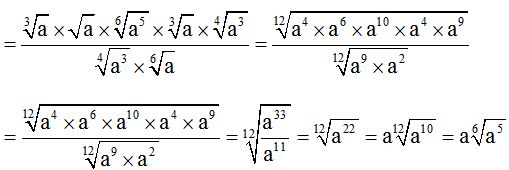Reducción a índice común.
Puede suceder que tengamos que multiplicar o dividir raíces con índices diferentes. Cuando éstos son iguales la multiplicación y división no produce ninguna dificultad:
10.68 Multiplica: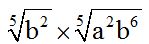 
Respuesta: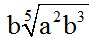 
Solución:
Para recordar lo tienes resuelto paso a paso.
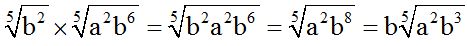
10.69 Calcula el cociente de:
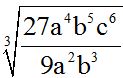Respuesta: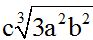 
Cuando los índices son diferentes se calcula el m.c.m. de ellos. Este valor se divide entre cada uno de los índices y el cociente se multiplica por cada uno de los exponentes del radicando.
10.70 Multiplica: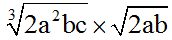 
Respuesta: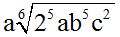 
.
Solución:
Los índices son 2 y 3. El m.c.m.(2 y 3) = 6
Al dividir 6 entre 3 tenemos 2 como cociente. Este cociente multiplicamos por los exponentes de cada uno de los factores del radicando del multiplicador.
Al dividir 6 entre 2 tenemos 3 como cociente. Este cociente multiplicamos por los exponentes de cada uno de los factores del radicando del multiplicador:
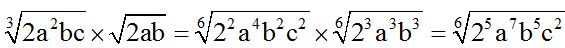
Siempre que puedas saca fuera de la raíz el factor que te lo permita:
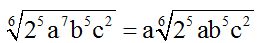
10.71 Multiplica: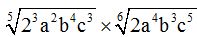 
.
Respuesta: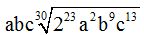 
10.72 Divide:
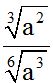Respuesta: 
.
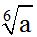Solución:
Calculamos el m.c.m.(3 y 6) = 6. Dividimos el m.c.m. entre cada índice y el cociente lo multiplicamos por cada exponente que tengamos en el radicando, después, reducimos términos semejantes si los hubiera. Para finalizar, dividimos el numerador entre el denominador teniendo en cuenta que para dividir potencias de la misma base restamos los exponentes:
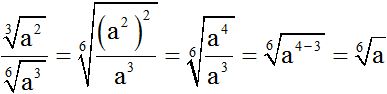
10.73 Calcula:
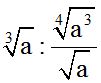Respuesta: 
.
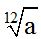Solución:
Sólo tenemos que tener en cuenta lo estudiado hasta ahora respecto a división de fracciones, división de potencias y raíces.
Tienes a continuación, el desarrollo de una forma de resolver el ejercicio:
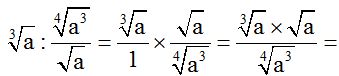
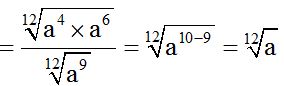
10.74 Halla el valor de:
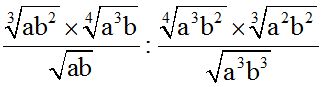Respuesta: 
.
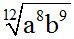Solución:
Tienes a continuación una forma de resolverlo, paso a paso:
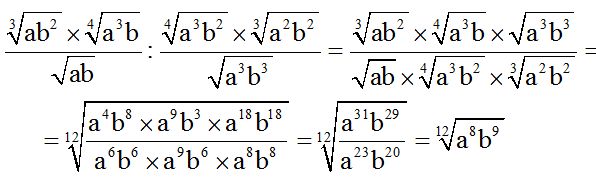
10.75 Halla el valor de:
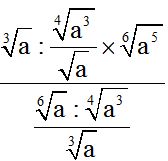Respuesta: 
.
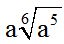Solución:
Un modo de resolver puede ser el siguiente:
