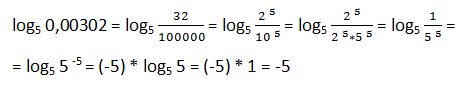Soluciones Ejercicios (2ª parte)
26. Calcula mediante logaritmos 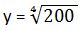
Solución:
Vamos a resolver este ejercicio aplicando logaritmos en base 3 pero podríamos hacerlo utilizando otra base cualquiera.
Aplicamos logaritmos a ambos miembros de la ecuación:
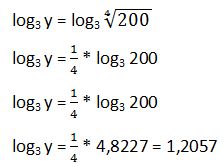
Aplicamos la fórmula del antilogaritmo:
y = antilog3 1,2057 = 3 1,2057 = 3,7606
27. Calcula mediante logaritmos 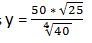
Solución:
Vamos a resolver este ejercicio aplicando logaritmos en base 2 pero podríamos hacerlo utilizando otra base cualquiera.
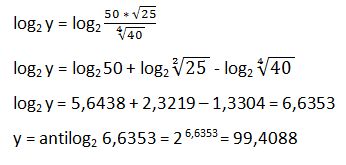
28. Calcula log 20 + log 5
Solución:
log 20 + log 5 = log (20 * 5) = log 100 = 2
29. Calcula 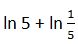
Solución:
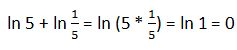
30. Aplicando la regla de cambio de base y utilizando logaritmo decimal resuelve: 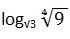
Solución:
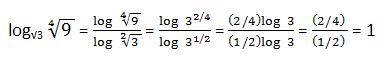
31. Calcula el valor de la base si 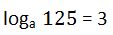
Solución:
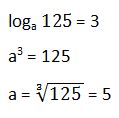
32. Calcula el valor del argumento si 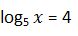
Solución:
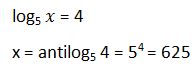
33. Utilizando la definición de logaritmo calcular: 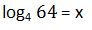
Solución:
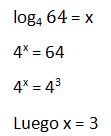
34. Utilizando la definición de logaritmo calcular: 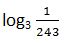
Solución:
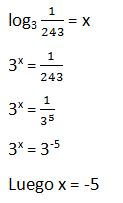
35. Calcula el valor de la base si 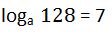
Solución:
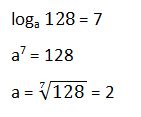
36. Calcula el valor de la base si 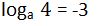
Solución:

37. Calcula el valor del argumento si 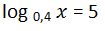
Solución:
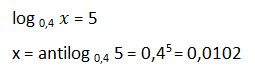
38. Calcula 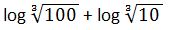
Solución:
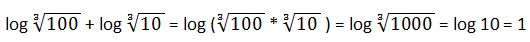
39. Calcula el logaritmo decimal log 50 en función del logaritmo en base 2:
Solución:
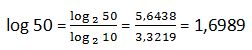
40. Calcular x en: log x = 2 + 3 * log 4
Solución:
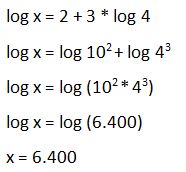
41. Calcular x en: log x + log x3 = 4
Solución:
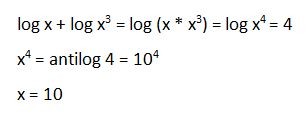
42. Calcula el valor de la base si 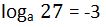
Solución:

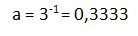
43. Calcula “x”: log2 x + log2 5 = 0
Solución:
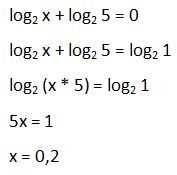
44. Calcula “x”: log x - log 3 = -4
Solución:
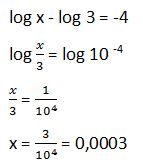
45. Calcula “x”: log 2 + log (2x – 4) = 2
Solución:
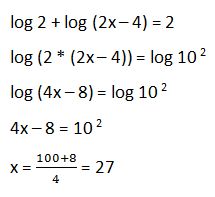
46. Calcula “x”: log (2x – 3) + 2 = log 3x
Solución:
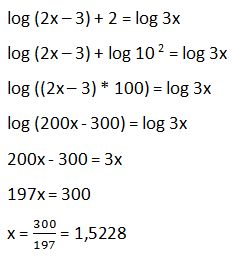
47. Si 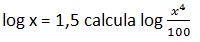
Solución:
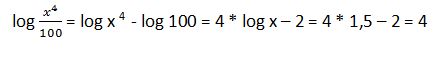
48. Resuelve: log2 16 – 2 log2 4 + log2 8
Solución:
log2 16 – 2 log2 4 + log2 8 =
log2 16 – log2 4 2 + log2 8 =
log2 16 – log2 16 + log2 8 =
49. Resuelve: log2 0,5
Solución:
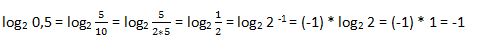
50. Resuelve: log5 0,00032
Solución: