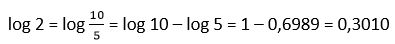Soluciones Ejercicios (1ª parte)

1. Si log₃ x = h, calcula log₃ 5x

Solución:

log₃ 5x = log₃ 5 + log₃ x = 1,4649 + h

2. Calcular log₂ 32 - log₂ 16

Solución:

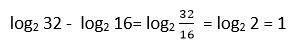
3. Sabiendo que log₄ 2 = 0,5 y log₄ 3 = 0,7924 calcula log₄ 6

Solución:

log₄ 6 = log₄ (2 * 3) = log₄ 2 + log₄ 3 = 0,5 + 0,7924 = 1,2924

4. Sabiendo que log₃ 2 = 0,6309 y log₃ 10 = 2,0959 calcula log₃ 5

Solución:

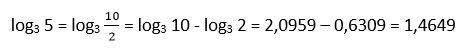
5. Sabiendo que log₄ 6 = 1,2924 y log₄ 3 = 0,7925 calcula log₃ 6

Solución:

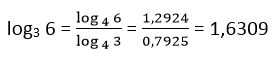
6. Calcular log₃ 81

Solución:

log₃ 81 = log₃ 3⁴ = 4 * log₃ 3 = 4 * 1 = 4

7. Calcular log_√3 9

Solución:

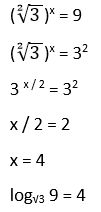
8. Calcular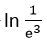

Solución:

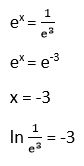
9. Calcular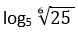

Solución:

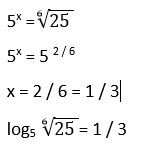
Otra alternativa:

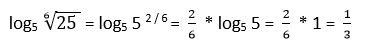
10. Calcular la base de log_a 64 = 4

Solución:

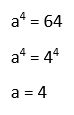
11. Calcular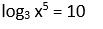

Solución:

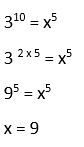
Otra alternativa:

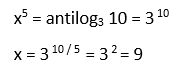
12. Calcular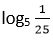

Solución:

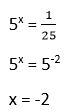
Otra alternativa:

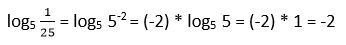
13. Calcular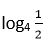

Solución:

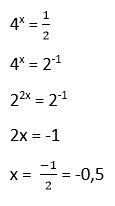
14. Calcular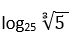

Solución:

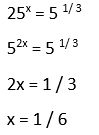
15. Calcular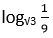

Solución:

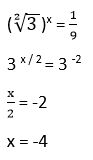
16. Calcular log₂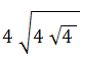

Solución:

   log₂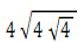

₌ log₂ 4 + log₂ 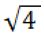+ log₂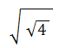

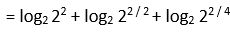
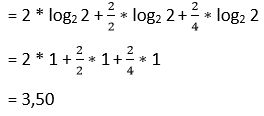
17. Calcular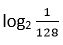

Solución:

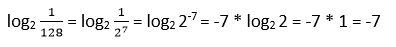
18. Calcular log 0,04

Solución:

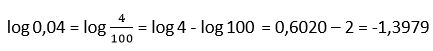
19. Calcular log₂ 7 * log₇ 2

Solución:

Expresamos los dos logaritmos en la misma base, luego:

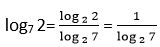
La expresión inicial queda:

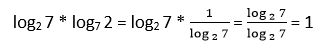
20. Escribir log₃ 10 en función de un logaritmo decimal y calcular:

Solución:

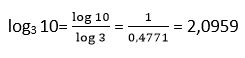
21. Escribir log5 en función de un logaritmo neperiano y calcular:

Solución:

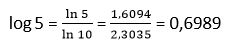
22. Calcula el valor de “y” aplicando las propiedades del logaritmo:

y = log _{1 / 3} 9

Solución:

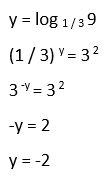
23. Calcula el valor de “y” aplicando las propiedades del logaritmo:

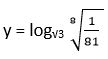
Solución:

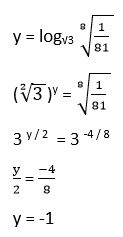
24. Si log 5 = 0,6989 calcula log 2

Solución: