La palabra vector procede de una palabra latina que significa "el que acarrea, el que lleva, el que transporta". Como ves, podemos traducir como el conductor, portador…
Se llama vector a un trozo, parte, porción o segmento de una recta pero que nos indica algo más que su longitud o módulo como son la dirección y el sentido. Sobre una recta x (sería la dirección) tomo un trozo, una parte o un segmento de la misma y señalo su longitud con las letras A y B y a la derecha le dibujo una flecha para indicar el sentido.
Los vectores se representan con las letras que determinan su módulo (comienzo y fin). En el ejemplo anterior, el comienzo del vector se encuentra en A y el final en B. Los vectores se representan con las letras de comienzo y fin del segmento con una recta con flecha sobre ellas indicando el sentido del desplazamiento 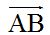 o una sola letra mayúscula o minúscula:
o una sola letra mayúscula o minúscula: 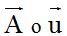 .
.
Muchas personas nos liamos con las palabras dirección y sentido.
El motivo es que cuando hablamos, utilizamos ambas palabras como si significasen lo mismo y no es así. Dirección es la línea donde se realiza un movimiento mientras que el sentido nos indica hacia dónde se realiza el movimiento, hacia uno u otro lado.
Imagina una carretera que va desde Almería a Granada, en este caso, nos referimos a la dirección. Esa carretera se podría haber trazado por otros lugares, es decir, que direcciones de Almería a Granada podrían existir muchas, pero en cada caso, solo habría dos sentidos o vamos hacia Granada o vamos hacia Almería. De un modo gráfico lo expresamos con el ejemplo siguiente
Las vías del tren nos indican la dirección. El tren o va en el sentido Madrid o en el sentido Irún. Direcciones puede haber muchas (lugares escogidos para trazar la línea del ferrocarril). Sentidos no puede haber más de dos.
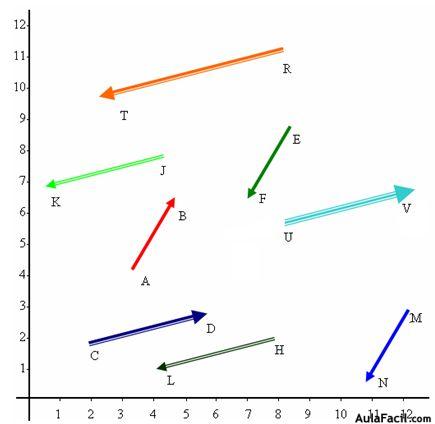
8.11 En este ejercicio tienes unos vectores que debes agruparlos:
1º por los que tienen iguales módulos
2º por los que tienen la misma dirección
3º por los que tienen el mismo sentido
Respuestas: Iguales módulos:
Iguales direcciones:
Iguales sentidos:
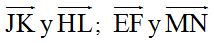
OPERACIONES CON VECTORES.
Sumar vectores:
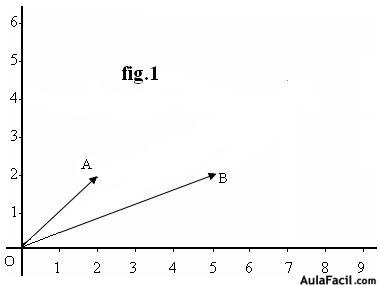
Para sumar dos o más vectores gráficamente unimos sus orígenes en un mismo punto tal como los tienes en la figura 1 en ella verás que los hemos hecho coincidir en el punto (0,0)
Vamos a sumar los vectores:
Es aconsejable que los dibujes en un eje de coordenadas
La suma puedes realizarla de dos modos:
a) gráficamente
b) sumando sus componentes.
Estas dos rectas se cortan en un punto C y este punto lo unes con el origen de las dos rectas y obtienes el vector 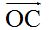 cuyo origen está situado en (0,0) y su extremo en (7,4)y es el resultado de la suma
cuyo origen está situado en (0,0) y su extremo en (7,4)y es el resultado de la suma 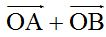 .
.
b) El extremo del vector 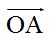 está situado en el punto(2,2) y el extremo del vector
está situado en el punto(2,2) y el extremo del vector 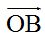 en (5,2). Los dos valores que definen a un punto, es decir, los valores de x y de y se llaman componentes (las componentes). Si sumamos ordenadamente las componentes de x e y tenemos (2+5,2+2) = (7,4) que es el valor obtenido gráficamente.
en (5,2). Los dos valores que definen a un punto, es decir, los valores de x y de y se llaman componentes (las componentes). Si sumamos ordenadamente las componentes de x e y tenemos (2+5,2+2) = (7,4) que es el valor obtenido gráficamente. 8.12 Sumar gráficamente los vectores 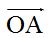 y
y 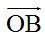 cuyas longitudes, direcciones y sentidos figuran en la figura a partir del punto (1,2).
cuyas longitudes, direcciones y sentidos figuran en la figura a partir del punto (1,2).
Solución:
En la figura 3 hemos colocado los dos vectores a sumar en un punto distinto de (0,0), se encuentra en el punto (1,2).
Resolvemos, figura 3, gráficamente por medio del trazado de las paralelas a ambos vectores a partir de A y B, como en el caso anterior. Se cortan en el punto C. Unimos este punto con O y tenemos el vector resultante de la suma de los vectores
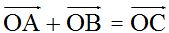
cuyas coordenadas corresponden al punto (8,6).
Esta respuesta no sería correcta porque hemos partido del punto (1,2). Esto quiere decir que hemos de restar las componentes de los puntos (8,6) y (1,2); (8,6) - ( 1,2) = (8 – 1, 6 – 2) = (7,4). Gráficamente tienes representados estos cálculos en la figura 4:
En el eje de ordenadas vemos que el punto C alcanza el valor 6, pero como ha partido desde el valor 2 y no desde el (0,0), en realidad su valor es de 6 – 2 = 4 y lo mismo sucede con el valor de la abscisa que alcanza el valor 8 pero ha partido desde el 1 y no desde (0,0) en cuyo caso tendremos que restarle 1 a 8 con lo que vemos que el valor de la suma es igual a (7,4).
El resultado es el mismo al obtenido al sumar sus componentes.
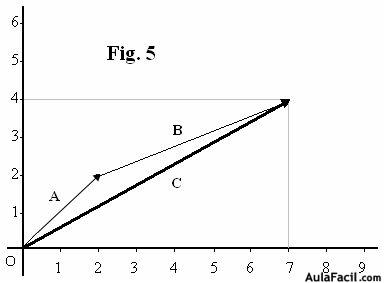
Otro modo de calcular una suma de vectores gráficamente es el de trasladar el segundo vector al final del vector primero y unir el origen del primer vector con el final del segundo.
Lo entenderás al observar la figura 5 donde hemos colocado el vector 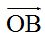 a continuación del vector
a continuación del vector 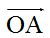 .
. Unimos el extremo del vector 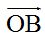 con el origen del vector
con el origen del vector 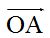 y obtenemos el vector
y obtenemos el vector 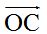 que corresponde a la suma de las componentes de los dos vectores
que corresponde a la suma de las componentes de los dos vectores 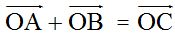 (7,4).
(7,4).
8.13 En el primer cuadrante de un eje de coordenadas cartesianas dibujas dos vectores y calculas la suma. Resuelve, al menos, de dos maneras diferentes.
Solución:
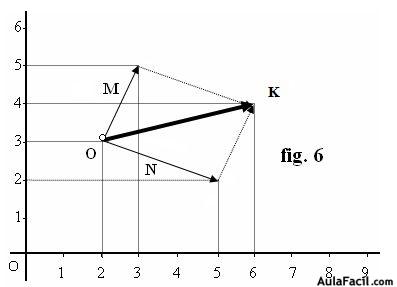
En la figura 6 suponemos dos y con vectores 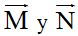 con origen, ambos en el punto(2,3) y final en (3,5) y (5,2) respectivamente En este caso representamos los vectores con una sola letra mayúscula
con origen, ambos en el punto(2,3) y final en (3,5) y (5,2) respectivamente En este caso representamos los vectores con una sola letra mayúscula
El resultado queda representado por el vector 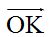 = (6,4)
= (6,4)
Sumando las componentes tenemos: (3+5, 5+2) = (8,7) pero este valor no procede del origen de coordenadas, del punto (0,0) sino del punto (2,3). A las componentes (8,7) hemos de restar las componentes (2,3) para que la medida proceda del punto (0,0):>
(8 – 2, 7 – 3) = (6,4).

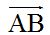 o una sola letra mayúscula o minúscula:
o una sola letra mayúscula o minúscula: 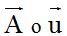 .
.
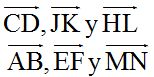
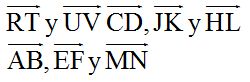
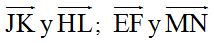

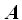 una paralela a
una paralela a 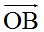
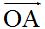 a partir de B como lo tienes en la figura 2
a partir de B como lo tienes en la figura 2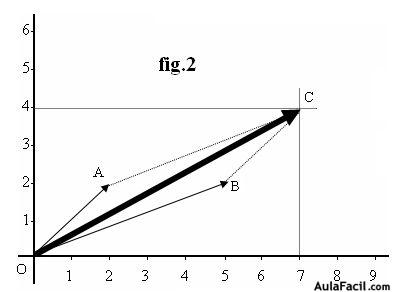
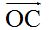
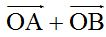 .
.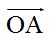
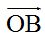
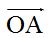 y
y 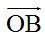 cuyas longitudes, direcciones y sentidos figuran en la figura a partir del punto (1,2)
cuyas longitudes, direcciones y sentidos figuran en la figura a partir del punto (1,2)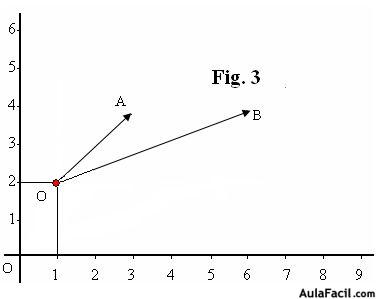

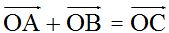 cuyas coordenadas corresponden al punto (8,6).
cuyas coordenadas corresponden al punto (8,6).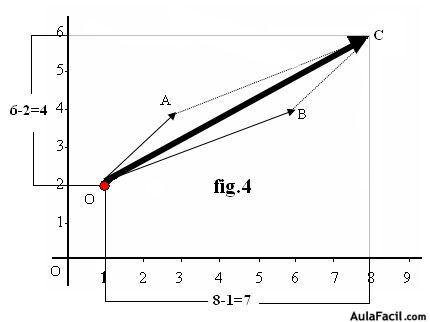
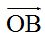 a continuación del vector
a continuación del vector 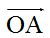 .
. 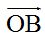 con el origen del vector
con el origen del vector 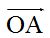 y obtenemos el vector
y obtenemos el vector 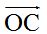 que corresponde a la suma de las componentes de los dos vectores
que corresponde a la suma de las componentes de los dos vectores 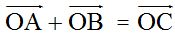 (7,4).
(7,4).
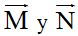 con origen, ambos en el punto(2,3) y final en (3,5) y (5,2) respectivamente En este caso representamos los vectores con una sola letra mayúscula
con origen, ambos en el punto(2,3) y final en (3,5) y (5,2) respectivamente En este caso representamos los vectores con una sola letra mayúscula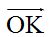 = (6,4)
= (6,4)
